what bs is this. Can someone plz explain to me how these r equal
View attachment 42231
Note that a purely geometric approach would provide the graph, with the points
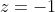
and
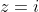
excluded, and is quicker:
} &= \pm \frac{\pi}{2} \\ \arg{(z -i)} - \arg{(z + 1)} &= \pm \frac{\pi}{2} \end{align*})
Geometrically, this statement tells us that the angle between the vector from
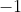
to

and the vector from
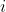
to

is a right angle.
Applying the converse of the angle in a semicircle theorem, it follows that

lies on one of the two semi-circles whose diameter is the interval joining
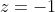
and
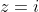
.
The two end points of the diameter,
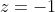
and
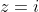
, are excluded from the locus as each results in one of the two vectors being the zero vector, and hence one of the two arguments being
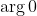
and thus undefined.
---
Taking the algebraic approach, the two constraints that lead to points being excluded are that
^2 + y^2 \neq 0)
and
(x + 1) - xy \neq 0)
. The point (-1, 0) violates both constraints, whilst the point (0, 1) violates only the second constraint.








