stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Has anyone attempted this?This one is tedious.
^2+\left(\pi+x\right)\left(\pi-x\right)\cos x+\pi^2\cos^2x}dx=\frac{1037\sqrt{2}+259\sqrt{3}-1893}{427})
To get the final answer, you have to express the annoying tangent in surd form.
Last edited:
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Has anyone attempted this?This one is tedious.
^2+\left(\pi+x\right)\left(\pi-x\right)\cos x+\pi^2\cos^2x}dx=\frac{1037\sqrt{2}+259\sqrt{3}-1893}{427})
That... doesn't necessarily have to be true, but my intuition agrees with that.If this integral has an elementary form, then there must be a relationship between p,q and r. After some trial and error, you would get that relationship.
No attempt for 2 weeksFeel free to share your attempt.
+\cos\left(\ln2\right)-\sin\left(2\ln2\right)-\cos\left(2\ln2\right)}{8}-\frac{\sin\left(\ln2\right)}{8\ln2}+\frac{\sin\left(2\ln2\right)}{16\ln2})
Math is not really my area but I tried nonethelessFeel free to share your attempt.
+\cos\left(\ln2\right)-\sin\left(2\ln2\right)-\cos\left(2\ln2\right)}{8}-\frac{\sin\left(\ln2\right)}{8\ln2}+\frac{\sin\left(2\ln2\right)}{16\ln2})
Math is not really my area but I tried nonetheless
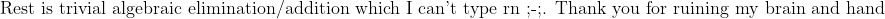
yeah I kinda realized that while going to sleep but I have no idea how to integrate sinx/x. so I kinda just went mehGood try!
Unfortunately, there's a mistake in this piece of integral.
Fortunately, it doesn't affect the final answer.
There's no closed form. Take a look at the upper and lower limits.yeah I kinda realized that while going to sleep but I have no idea how to integrate sinx/x. so I kinda just went meh
I still don't get what you mean by this...There's no closed form. Take a look at the upper and lower limits.
I KNEW IT. That's what I got but I thought I had made a mistake or something
Surely it can't be this simple?Using similar technique, it should be straight-forward to show that

