If you integrate an acceleration-time graph, you get the velocity.
Something to note : Differentiating displacement/distance-time graph gives velocity. Integrating gives nothing
differentiating velocity-time graph gives displacement/distance. Integrating gives acceleration
Differentiating acceleration-time graph gives nothing, Integrating gives velocity
Two points:
First, there is a typo above. The line "differentiating velocity-time graph gives displacement/distance. Integrating gives acceleration" is backwards, it should read that "differentiating velocity-time graph gives acceleration. Integrating gives displacement."
Second, be careful not to confuse distance and displacement. Displacement or position is given by
x and it has a direction, distance does not.
Example: Suppose a particle is moving according to
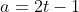
and it starts from rest at
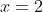
. Find the distance it travels in the first 2 seconds of motion.
We start with:

So, we know that the object starts at rest at
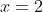
and after 2 seconds, reaches
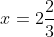
. It's displacement over this period is thus

of a unit in the positive direction from its starting point, but does this mean that the distance it has traveled is

? Not necessarily. If I get up from my desk, walk to the kitchen to get a drink, and then walk into the lounge room, my displacement is the change in position from desk to lounge room, but my distance traveled is further. For a distance calculation, I need to check if the object stops anywhere (as direction can only change when
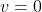
:
 &= 0 \end{align*})
We knew from the question that the particle was at rest at
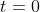
, but it is now clear that it is also at rest at
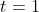
.
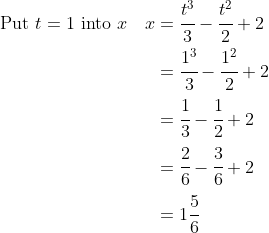
So, the particle starts at
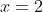
(at
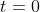
), moves to
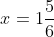
(at
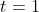
) where it changes direction (you can check by seeing that for
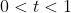
,
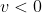
and after
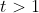
,
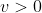
) reaching
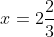
by
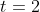
. It follows that the distance it travels in those 2 seconds is:
 + \bigg(2\cfrac{2}{3} - 1\cfrac{5}{6}\bigg) \\ &= (2 - 1) + \bigg(0 - \cfrac{5}{6}\bigg) + (2 - 1) + \bigg(\cfrac{2}{3} - \cfrac{5}{6}\bigg) \\ &=\bigg(1 - \cfrac{5}{6}\bigg) + 1 + \bigg(\cfrac{4}{6} - \cfrac{5}{6}\bigg) \\ &= \cfrac{1}{6} + 1 - \cfrac{1}{6} \\ &= 1 \end{align*})
Similar care needs to be taken in considering speed as opposed to velocity, or their averages.
