aa180
Member
For question 3, shouldn't  and
and 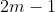 be coprime?
be coprime?
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Thanks for pointing this out. I have changed the files for both posts accordingly.For question 3, shouldn'tand
be coprime?
You're welcs. Does that now mean that everyone who sat the paper gets a free mark for it or nah?Thanks for pointing this out. I have changed the files for both posts accordingly.
I pray this is the last mistake/technical gap we have *sighs heavily*
eh; no, I doubt Trebla will go that way. Also nobody in the exam brought it up, so they must have made the implicit assumption as wellYou're welcs. Does that now mean that everyone who sat the paper gets a free mark for it or nah?
I had virtually no involvement in the papers this year. Too busy with other things. The other guys did a great job with filling in the gap that I've left!Wow this is definitely harder than the previous years. I see that Carrotsticks having extra assistance from former BOS members (who are also math whizzes) definitely revoluntionised the content.
However, with the new syllabus being implemented, I wonder what mathematical theorem do you plan to use that could be solved using strictly high-school math.
Gotta pay the bills right?Why is literally half of Bos a bunch of Math majors
dubiousThe other guys did a great job with filling in the gap that I've left!
Anyone manage to solve Q11a?
that is only worth one mark, you need to elaborate more
I didn't sit the paper, but here is my solution (spoilers for anyone who wants to solve)Anyone manage to solve Q11a?
LOLmeme post don't take seriously
View attachment 27310
>specifically says the base is less than 1
>mfw i see people drawing increasing exponentials instead of decreasing exponentials
Math isn't my area but isn't this the case???????apparently 90% of these students think that inverses that are tangent to each other are tangent to y=x. the syllabus teaches inverse functions so badly.

