Did all for fun... but still a bit rusty so it most likely has at least one error
____
We are only concerned on placement of Es so the sample space is
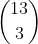
.
a) Group 3 Es as a blob. There are
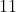
ways you can place this blob so the probability is
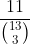
.
b) Group 2 Es as a blob. Suppose this blob (*) is at one end: * _ _ _ _ _ _ _ _ _ _ _. Then there are
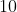
ways you can place the last E: * _
+ + + + + + + + + +, where the + represents a possible location for the remaining E. Similarly, there are
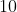
ways you can place the last E given that the blob is on the other end (symmetry).
Total # of ways if blob is at either end:
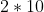
.
Suppose the blob is not at either ends. For example, _ * _ _ _ _ _ _ _ _ _ _. Then there are
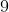
ways you can place the last
E: _ * _
+ + + + + + + + +.
It is clear that you can place this blob in
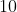
ways given that it's not at either ends.
Total # of ways if blob is not at either end:
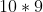
.
Probability is
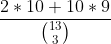
.
c) P(all Es apart) = 1 - P(all Es together) = 1 - [P(3 Es together) + P(2 Es together and one apart)] =
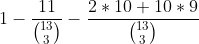
.
d) We have the following situation: E _ _ _ _ _ _ _ _ _ _ _ E. This initial position occurs in
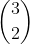
combinations. Then the remaining E can be placed in
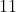
ways.
Probability is
* 11}{\binom{13}{3}})





