Kurosaki
True Fail Kid
http://community.boredofstudies.org/1125/mathematics-extension-1/330060/paper.htmlWould someone be able to upload the questions? We weren't allowed to take ours from the room!
Thanks.
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
http://community.boredofstudies.org/1125/mathematics-extension-1/330060/paper.htmlWould someone be able to upload the questions? We weren't allowed to take ours from the room!
Thanks.
The locus of Q is most definitely not a full circle.Carrotsticks, I doubt your parametric solution for Q13 (c) (iii).
you said: This is the equation of a circle centred at the focus with radius a. We have the condition that
x =/= 0 because this can only occur if P lies precisely on the vertex of the parabola ie: t = 0 .
However, when this happens, then we cannot define Q because having a ratio of 0 :1 yields
an undefined point.
But please check out the definition of ratio, 0:1 means 0/1 which has meaning (P and Q have no distance); 1/0 is meaningless
Also, when you put t=0 back into (i), the coordinates of Q becomes (0,0) which is on the circle we got in (iii), and it completes the circle. That's why the question says it's a full circle, BOS is not that stupid as you think. So imo, you do need to separate the cases where x=0 or not.
When x=0, t=0, but at this moment t is not the slope of OQ because at this moment Q is on origin, then OQ doesn't have a slope, so (ii) has no problem.
Thus the whole question is good. It may become a reason of some people losing state rank no1
Also a cool way of doing the second part of the circle geo question:
We want to show that OP is a tangent to the circle through PQC. Let there be a point D that lies on both the arc PC and the line OP extended.
We know that angle PAO = angle APO by isosceles triangles, and angle APO = angle DPC by vertically opposite angles, and thus angle PAO = angle DPC.
However angle PAO = angle CQP from part (i). Thus angle DPC = angle CQP, and so CD=PC by equal angles subtend equal arcs.
If CD=PC then the point P and D coincide and so, other then P, the line OP does not pass through any points on the circle PQC. Hence OP is a tangent.

Thank you for pointing out this erroneous statement. You are one of two students who have pointed this out. I am quite certain that the reason why I had made that mistake in the first place was because I had confused a ratio of 0:1 with the ratio 1:0 amongst the rush, without thinking about the bigger picture overall pointing out that the origin is most certainly a part of the locus equation.Carrotsticks, I doubt your parametric solution for Q13 (c) (iii).
you said: This is the equation of a circle centred at the focus with radius a. We have the condition that
x =/= 0 because this can only occur if P lies precisely on the vertex of the parabola ie: t = 0 .
However, when this happens, then we cannot define Q because having a ratio of 0 :1 yields
an undefined point.
But please check out the definition of ratio, 0:1 means 0/1 which has meaning (P and Q have no distance); 1/0 is meaningless
Also, when you put t=0 back into (i), the coordinates of Q becomes (0,0) which is on the circle we got in (iii), and it completes the circle. That's why the question says it's a full circle, BOS is not that stupid as you think. So imo, you do need to separate the cases where x=0 or not.
When x=0, t=0, but at this moment t is not the slope of OQ because at this moment Q is on origin, then OQ doesn't have a slope, so (ii) has no problem.
Thus the whole question is good. It may become a reason of some people losing state rank no1
Can you elaborate on your first line?The probability question part (ii):
since
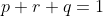
If person 1 has a probability of A of eventually winning, we note that person 2 must also have a probability of A of eventually winning given that person 1 does not win on his first turn.Can you elaborate on your first line?
omg this is exactly what i didthe probability question part (ii):
since
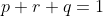
Best to confirm with Carret, but that sounds fine to mehey carrot, would you need to show that there were 2 solutions not just one for the ski jump question to find max d? because i showed the pi/8 and justified with 2nd derivative test, but i didnt include the 2nd possible solution. will the marker take marks off for this?
it'll be fine, because the question specified thatarghh so I showed that there were two stat points as 22.5 degrees (pi/8) and -67.5 degrees. I showed that the 22.5 degrees was a maxima by testing points around it, but just inspection of the other one in terms of the derivative told me that it was a minima so I didn't bother proving it (I wrote that it was a stationary point though).
Carrot do you think thats okay :/

even though im not carret i believe it was fudging as there was a legit way to figure it out lol. you may be lucky to get even 1 but definitely not more than that. remember the test wasn't very hard so marking will beCarrotsticks, for the parametric circle q, i didnt know how to use the previous part to find the curcle equation but I could immediately see that the centre was going to be S(0,a) so I just squared the X-coordinate of Q, subtracted a from the y co-ordinate (gave me [y-a]) and i squared that, then added both squares and the final term cancelled out to just a^2. Is that considered fudging? And would I still obtain full marks?

