-
Looking for HSC notes and resources? Check out our Notes & Resources page
Challenging (?) Proof Question (1 Viewer)
- Thread starter CM_Tutor
- Start date
If one wanted to actually find examples of 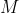 , here is an approach that works for
, here is an approach that works for 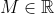 .
.
I'll use the hyperbolic function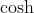 and its inverse, which aren't in the MX2 syllabus but their definitions are quite simple to understand:
and its inverse, which aren't in the MX2 syllabus but their definitions are quite simple to understand:
) and
and )
Now, let
 = x^n + \frac 1{x^n}) ,
,
be a real function where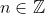 .
.
If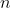 is even, then
is even, then  = f(-x)) .
.
If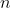 is odd, then
is odd, then =-f(-x) ) .
.
That is, the parity of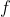 is the parity of
is the parity of 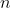 .
.
So without loss of generality, assume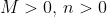 and make the substitution
and make the substitution 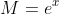 .
.
If = k) for some
for some 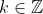 , then
, then
 , so
, so
 = \frac k2,)
.)
Since ,
,
 .
.
We require , which should be expected, as
, which should be expected, as 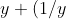 \ge 2 ) for all positive
for all positive 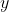 .
.
The original proposition

is equivalent (I believe) to
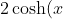 \in \mathbb Z \implies 2 \cosh(nx) \in \mathbb Z ) .
.
We also find an interesting identity:

for all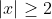 .
.
EDIT: It's worth noting that this shows that if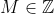 , then
, then 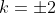 .
.
If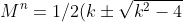) then
then 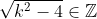 .
.
The gap between the second and third perfect square is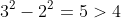 , and this gap will only increase as you go further out.
, and this gap will only increase as you go further out.
So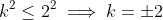 . Subbing in these values confirms that
. Subbing in these values confirms that 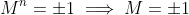 .
.
I'll use the hyperbolic function
Now, let
be a real function where
If
If
That is, the parity of
So without loss of generality, assume
If
Since
We require
The original proposition
is equivalent (I believe) to
We also find an interesting identity:
for all
EDIT: It's worth noting that this shows that if
If
The gap between the second and third perfect square is
So
Last edited:
ewjfiwhelowaeoplg
New Member
- Joined
- Mar 30, 2020
- Messages
- 13
- Gender
- Undisclosed
- HSC
- 2020
Yes, strong induction is the standard X2 approach for these sorts of questions
There is one other possibility,Is the conditionreally necessary?
The only case of this I can see is, so it would be simpler to leave it unmentioned.
On reflection, the result is also true if the restriction on n is simply
I agree that the induction approach noted by ultra908 is the obvious / standard approach. The approach from fan96 is not one I had considered, but it's also beyond the MX2 syllabus. Are there any other approaches anyone would consider?
You could go into complex numbers and use Taylor series expressions for real and imaginary part, then you could prove local finite integer ABSOLUTE convergence from a point, calling z_n = M^n + M^(-n) and by proving that |Re(z_n)| and |Im(z_n)| ==> |z_n| converges. Type of approach from complex analysis.Prove that ifbut
, then
for all
.
I am curious as to how Extension 2 students would approach this as a proof problem, and wondering if there are other approaches beyond the two that occur to me.
Yes, it will work, but it is effectively a strong induction proof:Does my Binomial expansion not work, cus that and Induction is the only way My small brain can think off. was thinking of complex numbers too since its in that form but yeah haha
Now, applying the symmetry property that
Now, the last term in this series of sums depends on whether
Whether
I was thinking about a proof like this: The quadratic equation with roots at  is
is
\big(x - M^{-1}\big) = 0) , which expands and rearranges to give
, which expands and rearranges to give x - 1)
It follows that
We then prove that , with or without using induction,
, with or without using induction,
because that gives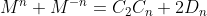 must be an integer.
must be an integer.
It follows that
We then prove that
because that gives
Paradoxica
-insert title here-
This is completely valid but technically requires induction to complete the argument for all naturals.I was thinking about a proof like this: The quadratic equation with roots atis
, which expands and rearranges to give
It follows that
We then prove that, with or without using induction,
because that givesmust be an integer.
The logic is inductive, I agree, though it doesn't actually need to be presented as an induction proof.This is completely valid but technically requires induction to complete the argument for all naturals.
