-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Counting Q (1 Viewer)
- Thread starter QZP
- Start date
Why?
aDimitri
i'm the cook
basically if those are the prime factors, you can include any of them in a divisor raised to any integer power, maximum being the index of the prime factors, but also including ^0.
so an example of a diviser would be 2^0 * 3^2 * 5^3 * 7^0
then it's just fundamental counting theory multiply the combinations together.
Thanks 
I had a similar idea considering 10 elements {2,2,2,3,3,...,7} and then choosing from there but I couldn't figure out how (tried to do like 10C0 + 10C1 + ... + 10C10 but then didn't know how to remove duplicates)
Anyone know how to do the the one in the opening post?
I had a similar idea considering 10 elements {2,2,2,3,3,...,7} and then choosing from there but I couldn't figure out how (tried to do like 10C0 + 10C1 + ... + 10C10 but then didn't know how to remove duplicates)Anyone know how to do the the one in the opening post?
RealiseNothing
what is that?It is Cowpea
Choose all 6 vertices without assigning them to a specific triangle. Done in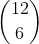 
ways.
Now you want to assign these points to the 2 triangles without overlapping the areas. Thus the vertices must be assigned in cyclic order. i.e. going around the vertices in order of where they lie on the circle, assign the first 3 vertices to the first triangle and the last 3 to the second triangle.
This is done in 3 ways.
So answer is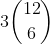
Rushed this so hopefully I haven't miscounted the amount of ways to assign the vertices.
Now you want to assign these points to the 2 triangles without overlapping the areas. Thus the vertices must be assigned in cyclic order. i.e. going around the vertices in order of where they lie on the circle, assign the first 3 vertices to the first triangle and the last 3 to the second triangle.
This is done in 3 ways.
So answer is
Rushed this so hopefully I haven't miscounted the amount of ways to assign the vertices.
aDimitri
i'm the cook
group 2 E's, do prob as though they are 1 letter, then subtract the answer from 14a
basically 2 E's together is inclusive of 3 E's together so you can subtract it.
basically 2 E's together is inclusive of 3 E's together so you can subtract it.
aDimitri
i'm the cook
is it not possible to have triangle 1 be made up of {6,1,2} and triangle 2 made up of {3,4,5} ?Choose all 6 vertices without assigning them to a specific triangle. Done in
Now you want to assign these points to the 2 triangles without overlapping the areas. Thus the vertices must be assigned in cyclic order. i.e. going around the vertices in order of where they lie on the circle, assign the first 3 vertices to the first triangle and the last 3 to the second triangle.
This is done in 3 ways.
So answer is
Rushed this so hopefully I haven't miscounted the amount of ways to assign the vertices.
Kurosaki
True Fail Kid
Treat 2 E's as one unit. You can arrange them together in 1 way.
Arrange everything else first:
You have 11 gaps to insert EE and E into, which means there are
Therefore arrangements with two E's together and one apart=
divide by total number of arrangements and you should get it.
aDimitri
i'm the cook
or thisTreat 2 E's as one unit. You can arrange them together in 1 way.
Arrange everything else first:ways.
You have 11 gaps to insert EE and E into, which means there areways to insert them in.
Therefore arrangements with two E's together and one apart=.
divide by total number of arrangements and you should get it.
RealiseNothing
what is that?It is Cowpea
That was counted in my solution.
NiceChoose all 6 vertices without assigning them to a specific triangle. Done in
Now you want to assign these points to the 2 triangles without overlapping the areas. Thus the vertices must be assigned in cyclic order. i.e. going around the vertices in order of where they lie on the circle, assign the first 3 vertices to the first triangle and the last 3 to the second triangle.
This is done in 3 ways.
So answer is
Rushed this so hopefully I haven't miscounted the amount of ways to assign the vertices.
Very cleanThat is the same outcome as triangle 1 made up of {3,4,5} and triangle 2 made up of {6,1,2}.
aDimitri
i'm the cook
yeah nvm this was not what i was confused about, i just made a stupid mistake in my solution
I have another Q that I feel doesn't deserve a new thread:
"There are two distinct round tables, each with five seats. In how many ways may a group of ten people be seated?"
How would you set the "reference point" for each table? With one table you just use a random person but idk here
"There are two distinct round tables, each with five seats. In how many ways may a group of ten people be seated?"
How would you set the "reference point" for each table? With one table you just use a random person but idk here
aDimitri
i'm the cook
That's probably the answer they want, but whoever thought up these two table questions has no idea.
The whole concept of relative positions is lost once you add a second table.
Unless we put a divider between the tables so they can't see each other.