How did you get U being a subset of C? (It would be the other way around in general.)
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Discrete Maths Last Minute questions (1 Viewer)
- Thread starter Drsoccerball
- Start date
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Because we have:How did you get U being a subset of C? (It would be the other way around in general.)
Ah right yeah, didn't read it carefully before. But I think your earlier steps are dodgy or strangely worded. Here's a way to do it.Because we have:

Assume the hypotheses about A,B,C and let x be in A. If x is also in B, then x is in A∩B, which implies it's in C (since A∩B ⊆ C). If x is not in B, then x is in A – B, which implies it's in C (as A – B ⊆ C). Hence either way, x is in C, whence A ⊆ C.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
That's much more straightfoward. But I still think my way is perfectly valid can't see anything wrong with itAh right yeah, didn't read it carefully before. But I think your earlier steps are dodgy or strangely worded. Here's a way to do it.
Assume the hypotheses about A,B,C and let x be in A. If x is also in B, then x is in A∩B, which implies it's in C (since A∩B ⊆ C). If x is not in B, then x is in A – B, which implies it's in C (as A – B ⊆ C). Hence either way, x is in C, whence A ⊆ C.
Thanks
Possibly your intentions may have been valid, but I'm not exactly sure what you meant by your wordings. Like what did you mean when you wrote for example "Either x ∈ A ⟺ x ∈ C" near the beginning? Note also that C doesn't have to be the universal set, but it turns out that C just has to be a superset of (i.e. have as a subset) A (which is what we needed to prove). E.g. if A = {1, 2}, B = {2, 3}, and C = {1, 2, 3, 4}, then A \ B = {1} ⊆ C and A∩B = {2} ⊆ C, but it need not be that C be the universal set (since the universal set may be the set of all positive integers for example). It wouldn't then hold that Bc ⊆ C.That's much more straightfoward. But I still think my way is perfectly valid can't see anything wrong with it
Thanks
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
If x is and element of A then x is also an element of C (a is a subset of C). I think instead of writing "or" I should've wrote "and" as it is an intersection. So the last step is not required and the proof pretty much is your proof. (Just got confused with and/or).
Edit: If it was union instead of intersection I think the last step I did would be required right?
Edit: If it was union instead of intersection I think the last step I did would be required right?
To say this with an arrow, we should use an arrow like this: ⇒. This arrow means "if ... then" (i.e. "implies"). The one you used (double-sided arrow) instead means "if and only if" (makes sense, since that arrow goes both ways).If x is and element of A then x is also an element of C
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
I was more trying to say this implies is that the same thing?To say this with an arrow, we should use an arrow like this: ⇒. This arrow means "if ... then" (i.e. "implies"). The one you used (double-sided arrow) instead means "if and only if" (makes sense, since that arrow goes both ways).
"Implies" is the "if...then" (these two are the same thing) and should be written with a "⇒" arrow if you use an arrow.I was more trying to say this implies is that the same thing?
"If and only if" is different (as it goes in both directions) and is denoted with an "⟺" arrow.
The "⟺" arrow can't be used for "implies", and the "⇒" arrow can't be used to mean if and only if. (Because these are two very different things.)
Suppose that 26 integers are chosen from the set S={1, 2, ..., 50}
By writing these numbers as 2km with m odd, prove that one of the chosen numbers is a multiple of another of the chosen numbers.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Hmm interesting, the values of k are going down.
But the more obvious pattern of k going down by 1 seems to halt...
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
The way I did it was that the worst case scenario is when we pick {26,27,...,50} since none are multiples of the other and by the pigeon hole principle we have to pick another number which is a multiple of one of the other numbers already picked.
Hmm interesting, the values of k are going down.
But the more obvious pattern of k going down by 1 seems to halt...
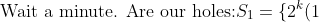\}\\ S_3=\{2^k(3)\}\\ \vdots\\ S_{25}=\{2^k(25)\})
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
What I did was :Consider the 10 letter word PARRAMATTA and all the words formed by rearranging its letters. How many of these words contain the subword MAP but not the subword RAT?
They gave no answer so I'm asking for checking:

Words which contain map - words which containt map and rat (Also take note that rat can appear twice) + missing
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Good observation. Also in my working that + should've been a minus but I need to do redo the whole thing anyway cause of the incl/exclWhat I did was :
Words which contain map - words which containt map and rat (Also take note that rat can appear twice) + missing
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Its funny because I only picked that up when writing my though pattern lel... Need help for the examGood observation. Also in my working that + should've been a minus but I need to do redo the whole thing anyway cause of the incl/excl
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Just to compare answers I got :Good observation. Also in my working that + should've been a minus but I need to do redo the whole thing anyway cause of the incl/excl
