-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Extension One Revising Game (1 Viewer)
- Thread starter conics2008
- Start date
Pwnage101
Moderator
it might be quiker not to square,. because the the numerator AND the denomenator are both positive, since they are both absoulte values. Then you could take cases.what are u doing staying up so late ??
Anyway here's my attempt:
Hopefully answer correct.
But yeh your method is fine.
Dragonmaster262
Unorthodox top student
I fell asleep early and woke up in the middle of the night.what are u doing staying up so late ??
Anyway here's my attempt:
Hopefully answer correct.
jet
Banned
- Joined
- Jan 4, 2007
- Messages
- 3,148
- Gender
- Male
- HSC
- 2009
Okay, Parabola, 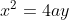
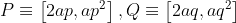
Prove that pq = -1 if the chord PQ passes through (0,a) and hence find the locus of R, the intersection of the normals at P and Q, if the chord passes through the point (0, a). The equation of the chord isx - apq) . You must prove all other formulas. [5 Marks]
. You must prove all other formulas. [5 Marks]
Prove that pq = -1 if the chord PQ passes through (0,a) and hence find the locus of R, the intersection of the normals at P and Q, if the chord passes through the point (0, a). The equation of the chord is
gurmies
Drover
NEW QUESTION:
Last edited:
[maths]r\binom{n}{r}=\frac{rn!}{r!(n-r)!}=n\frac{(n-1)!}{(r-1)!(n-r)!}=n\binom{n-1}{r-1}[/maths]
[maths]P_1+P_2+P_3+...+P_n\\=\sum_{r=1}^{n}\binom{n}{r}x^r(1-x)^{n-r}\\=(1-x+x)^n\\=1[/maths]
[maths]P_1+2P_2+3P_3+...+nP_n\\=\sum_{r=1}^{n}r\binom{n}{r}x^r(1-x)^{n-r}\\=\sum_{r=1}^{n}n\binom{n-1}{r-1}x^r(1-x)^{n-r}\\=nx\sum_{r=1}^{n}\binom{n-1}{r-1}x^{r-1}(1-x)^{n-r}\\=nx(1-x+x)^{n-1}\\=nx[/maths]
New Question:
Differentiate x^x with respect to x.
[maths]P_1+P_2+P_3+...+P_n\\=\sum_{r=1}^{n}\binom{n}{r}x^r(1-x)^{n-r}\\=(1-x+x)^n\\=1[/maths]
[maths]P_1+2P_2+3P_3+...+nP_n\\=\sum_{r=1}^{n}r\binom{n}{r}x^r(1-x)^{n-r}\\=\sum_{r=1}^{n}n\binom{n-1}{r-1}x^r(1-x)^{n-r}\\=nx\sum_{r=1}^{n}\binom{n-1}{r-1}x^{r-1}(1-x)^{n-r}\\=nx(1-x+x)^{n-1}\\=nx[/maths]
New Question:
Differentiate x^x with respect to x.
study-freak
Bored of
- Joined
- Feb 8, 2008
- Messages
- 1,128
- Gender
- Male
- HSC
- 2009
[maths]\int_{0}^{\pi/4}(\cos x+\sec x)^2dx\\=\int_{0}^{\pi/4}(\cos^2x+sec^2x+2)dx\\=\int_{0}^{\pi/4}(\frac{5}{2}+\frac{1}{2}\cos2x+\sec^2x)dx\\=[\frac{5}{2}x+\frac{1}{4}\sin2x+\tan x]^{\pi/4}_0\\=\frac{5\pi}{8}+\frac{5}{4}[/maths]
New Question:
Find @ if the quadratic y=ax(x-1) is tangent to circle x^2 + y^2 = 1 at x=@.
New Question:
Find @ if the quadratic y=ax(x-1) is tangent to circle x^2 + y^2 = 1 at x=@.
Last edited:
if you draw the parabola, and the circle, then if they're tangent, the line from the origin to @ must be perpendicular to the tangent (circle geo property).Find @ if the quadratic y=ax(x-1) is tangent to circle x^2 + y^2 = 1 at x=@.
the gradient of that line is a@(@-1)/@ = a(@-1)
by differentiating we find the gradient of the tangent to be a(2@-1)
so a^2(@-1)(2@-1) = -1 (perpendicular gradients)
a^2 = 1/(1-@)(2@-1)
then, we have
1-@^2 = a^2@^2(1-@)^2
1+@ = @^2(1-@)/(1-@)(2@-1)
= @^2/(2@-1)
(1+@)(2@-1) = @^2
@^2 + @ - 1 = 0
@ = -1/2 +- rt(5)/2
and from the diagram we can see that @ must be positive, so @ = -1/2 + rt5 /2
is there a simpler way to solve this?
my ext teacher sed that we couldnt expand brackets in inequalitieswhat are u doing staying up so late ??
Anyway here's my attempt:
Hopefully answer correct.
addikaye03
The A-Team
Posting a Q on behalf of lolokay, Question:
For the Geometric series a+ar+ar^2+...
Show that if lim(n-->infinite) Sn=S, then S-Sn=ar^n/1-r
Hence, find the least value of n for which (S-Sn) for the series 6+3+1.5+...is less than 0.0001.
For the Geometric series a+ar+ar^2+...
Show that if lim(n-->infinite) Sn=S, then S-Sn=ar^n/1-r
Hence, find the least value of n for which (S-Sn) for the series 6+3+1.5+...is less than 0.0001.
addikaye03
The A-Team
Remember that|a|=rt(a^2)my ext teacher sed that we couldnt expand brackets in inequalities
Don't understand. Can u plz elaborate.my ext teacher sed that we couldnt expand brackets in inequalities
Dragonmaster262
Unorthodox top student
Find x:
5^2x-5^x-20
5^2x-5^x-20
study-freak
Bored of
- Joined
- Feb 8, 2008
- Messages
- 1,128
- Gender
- Male
- HSC
- 2009
insufficient information unless you mean 5^2x-5^x-20=0Find x:
5^2x-5^x-20
and I guess you actually mean 5^(2x)-5^x-20=0?
S= S {inf} = (a/(1-r))Posting a Q on behalf of lolokay, Question:
For the Geometric series a+ar+ar^2+...
Show that if lim(n-->infinite) Sn=S, then S-Sn=ar^n/1-r
Hence, find the least value of n for which (S-Sn) for the series 6+3+1.5+...is less than 0.0001.
S-S{n}
= (a/(1-r)) - (a(r^n-1)/r-1)
= (a/(1-r)) - (a(1-r^n)/r-1)
= (ar^n)/(1-r)
S-S{n} < 0.0001
(ar^n/1-r) < 0.0001
(6(1/2)^n/(0.5)) < 0.0001
(1/2)^n < (0.0001/12)
n < ln(0.0001/12)/ln(1/2)
n < 16.87...
Thus, n is 16.
I don't think my answer is right though.
Last edited:
