Help? (1 Viewer)

[miniwaybzz]

hey guys,
can anyone help me with the 05 paper Q6)iii) [FML stuck on a q6 question ]

V = 3600 ( 1 - t/60 ) ^2 where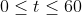
At what time does the model predict that the water will drain from the
tank at its fastest rate?

How do we approach this? fastest rate? so since rate = first derivative , we find 2nd derivative for maximum ? :S

thanks

 

[krnofdrg]

DV/DT= -120(1-t/60)

=-120+2t

To find when water will drain faster , consider d2v/dt2:

D2v/dt2= 2

Since, d2v/dt2 is a constant, check end-points:

when t=0, dv/dt = -120

t=60, dv/dt= 0

Therefore the water will drain at the fastest rate when t=0.

 

[miniwaybzz]

Since, d2v/dt2 is a constant, check end-points:

ahhh okay. ive never used/seen that method before...... , can you please explain the reasons for checking specifically, endpoints?

 

[krnofdrg]

ahhh okay. ive never used/seen that method before...... , can you please explain the reasons for checking specifically, endpoints?

If the second derivative comes out a constant such as in this case, then you must sub in the values of 'T' in your case is 60 and 0 into the first derivative equation to find the fastest rate. As you cannot sub any value into '2'...

Spiralflex can confirm on this one!

 

[miniwaybzz]

ok, but how do we know that the max point or fastest rate isnt a value inbetween 0 and 60min ? like 30min or something?

 

[D94]

Just look at the first derivative: -120 + 2t. The first derivative is the rate at which the water is draining, so when t = 0, it has maximum drainage, ie. -120 (the negative sign means the water being taken out/drained/reduced).

 

[miniwaybzz]

ahh okay i see now thanks