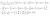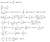Re: MX2 Integration Marathon
Edit: Oops, left out a few logs. But I can't be bothered fixing it.
Solution: View attachment Integral of ln (sinx).pdf
(without using complex numbers)
Edit: Oops, left out a few logs. But I can't be bothered fixing it.
Last edited: