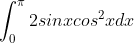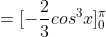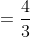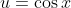Re: 2012 HSC MX1 Marathon
Carrotsticks, I am still unsure on how you determined the nature of the roots i.e. which ones were real and which ones were complex?
A cubic always has 3 roots. The question is, how many of them are real?
Case #1: All 3 roots are real and
distinct (meaning no two roots are the same)
Case #2: All 3 roots are real, but not all are distinct (This is the case when there's a double root and a single root)
Case #3: 1 root is real, but the others are complex (We MUST have at least 2 real roots because all the coefficients are real, meaning that the conjugate root theorem kicks in)
Now, we found that the sum of roots (squared) is equal to 1.
Suppose we have Case #1:
All 3 roots must be within the interval 0 < x < 1 in order for the sum of them (squared) to be equal to 1. The roots could be positive, but when squared it will be positive. They could ALL be negative. However when squared, they will still be positive! The moment one of the roots exceeds 1, the sum of the squares of the other 2 roots must be negative to 'balance' it. However, it's impossible for the other 2 roots to be real, since the only numbers that give negative values when squared... are complex numbers!
Suppose we have Case #2:
Again, both roots must be within the interval 0 < x < 1 (which in short is denoted by (0,1). If I use a square bracket [0,1], it means it is inclusive).
The trivial case would be to have a double root at 0, and the single root at 1 (or visa versa). However by simply substituting x=0 and 1 into the equation, we can see that roots occur at neither.
This means that the double root AND the single root has to FIT within the interval (0,1), which is very unlikely. Reason being, (0,1) is a small interval, and the coefficients of the polynomial look too 'normal' for anything weird like that to occur.
This leaves Case #3, which is how I made my deduction (and it is the most probabilistic solution).