Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (3 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Yeah that sounds more correct, thank youThink you meant:
prove that x is a Fibonacci number if and only if 5x^2+4 or 5x^2-4 is a perfect square. (just being picky).
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Re: HSC 2013 4U Marathon
Think of the subsets of as picking
as picking  elements from the set. That is, if you choose 0 elements, you have 1 choice. If you choose 1 element, you have n choices, for 2, nC2. Ie:
elements from the set. That is, if you choose 0 elements, you have 1 choice. If you choose 1 element, you have n choices, for 2, nC2. Ie:  which is clearer from your point of view from the expansion of
which is clearer from your point of view from the expansion of ^n.) On replacement of n by 2n we get the result.
On replacement of n by 2n we get the result.
Think of the subsets of
rural juror
New Member
- Joined
- Feb 24, 2013
- Messages
- 16
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
looking at x^6(y^-2 - x^-2) > y^6(y^-2 - x^-2) *just assume the greater than sign is greater than or equal to, this inequality can be easily shown for x>y and y>x to hold true, then all you have to do is move the fractions over and you have the result. max 3 lines or so
i might have a quicker way and easier to find,We know that:
Now letand
Multiply both sides by 3 to establish the inequality:
Now consider:
Split the RHS up into the following:
Now using the inequality we establish before, we get:
Let this be A:
Hence since
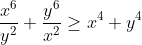
looking at x^6(y^-2 - x^-2) > y^6(y^-2 - x^-2) *just assume the greater than sign is greater than or equal to, this inequality can be easily shown for x>y and y>x to hold true, then all you have to do is move the fractions over and you have the result. max 3 lines or so
rural juror
New Member
- Joined
- Feb 24, 2013
- Messages
- 16
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
oh same solution as sys thatll teach me to scroll down
oh same solution as sys thatll teach me to scroll down
Re: HSC 2013 4U Marathon
dx \\ \\ = \int ^a _0 tan^{2n-1}x sec^2x dx - \int ^a _0 tan ^{2n-1}xdx \\ \\ = \left [\frac {tan ^{2n} }{2n} \right ] ^a _0- I_{n-1} = \frac {1}{2n} - I_{n-1}\\ \\ I_0 = \int ^a _0 tan x dx = \left [ -ln |cos x| \right ] ^a _0 = ln \sqrt 2 \\ \\ I_n = \frac {1}{2n} - I_{n-1} = \frac {1}{2n} - \frac {1}{2(n-1)} + I_{n-2} = \cdots \\ \\ = \frac {1}{2n} - \frac {1}{2(n-1)} + \frac {1}{2(n-2)} - \cdots + \frac {(-1) ^{n-1}}{2} - I_0\\ \\ = \frac {1}{2} \sum ^n _1 \frac {(-1) ^{(n-1)}}{n} - I_0 \\ \\ $Now $ 0 < I_n \leq \int _0 ^a ( \frac {4x}{\pi}) ^n dx = \left [ (\frac {4}{\pi})^ n \frac {x}{n+1} \right ] ^ {\frac {\pi}{4}} _0 = \frac {\pi}{4(n+1)} \to 0 $ as n $ \to \infty.\\ \\ \therefore $ by the Sandwich Theorem $ \\ \\ \lim _{n \to \infty} I_n = 0 \implies \sum ^\infty _{n=1} \frac {(-1) ^{n-1}}{n} = 2 \times I_0 = 2 \times ln \sqrt 2 = ln 2 )
Above solution messy and may contain errors. Have been making it up as I went along.
Above solution messy and may contain errors. Have been making it up as I went along.
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

Yep that is correct.
Maybe not quite correct yet. May need to have a look at it again
Re: HSC 2013 4U Marathon
(n^2-10n+100) - 900 \ $)


Are you sure this one is correct? I'm fairly certain I can prove it has a lower bound of 9 and an upper bound of 90 pretty easily...
First post, let's see if I can get the latex right -- I'm studying how you've done it lol
Are you sure this one is correct? I'm fairly certain I can prove it has a lower bound of 9 and an upper bound of 90 pretty easily...
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Feel free to post your proof of the upper and lower bounds though
EDIT: Yeah my proof is wrong, I didn't consider the numbers where a zero is in the middle -.-
The first answer is correct, as for the second one, let me check my proof again, I got the result from 'Art of Problem SOlving' and it asked whether it diverged and converged.First post, let's see if I can get the latex right -- I'm studying how you've done it lol
Are you sure this one is correct? I'm fairly certain I can prove it has a lower bound of 9 and an upper bound of 90 pretty easily...
Feel free to post your proof of the upper and lower bounds though
EDIT: Yeah my proof is wrong, I didn't consider the numbers where a zero is in the middle -.-
Last edited:
rural juror
New Member
- Joined
- Feb 24, 2013
- Messages
- 16
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Is it (-1)^n-1*n!*k^n???Another good Putnam question
 )
fionarykim
Member
- Joined
- Jul 21, 2012
- Messages
- 264
- Gender
- Female
- HSC
- 2013
Re: HSC 2013 4U Marathon
How are u guys typing so much maths here LOOOL im amazed
Also the questions just seem to just confuse my head, too hard ):
How are u guys typing so much maths here LOOOL im amazed
Also the questions just seem to just confuse my head, too hard ):
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
rural juror
New Member
- Joined
- Feb 24, 2013
- Messages
- 16
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
seemed a bit on the easy side for putnam surely???
seemed a bit on the easy side for putnam surely???
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
I thought so too, its problem A1 for 2002 iirc.seemed a bit on the easy side for putnam surely???
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

- Status
- Not open for further replies.

