Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
$ \\ \frac{x+y}{2} \geq \sqrt{xy} \ \ (1) \ , \frac{y+z}{2} \geq \sqrt{yz} \ \ (2) \ , \ \frac{x+z}{2} \geq \sqrt{xz} \ \ (3) \\ \\ (1) \cdot (2) \cdot (3) \\ \\ \Rightarrow \ (x+y)(x+z)(y+z) \geq 8xyz \ \square )
 \\ a+c \leq b \Rightarrow \ -b \leq -a-c \ (2) \\ \\ (1) + (2) \Rightarrow \ \therefore \ a+b-b \leq -a-c+c \Rightarrow \ a\leq -a \Rightarrow \ a\leq 0 \\ \\ $Similary we do the same to get$ \ b \leq 0 \ $and$ \ c \leq 0 \\ \\ $But since$ \ a,b,c \geq 0 \Rightarrow \ a=b=c=0 \\ \\ $Meaning$ \ 0 \geq 0 \ $which is true$ \ \square )
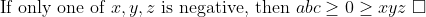
EDIT: There is a small error with my solution when looking to the case that at least 2 of x,y,z are negative, it has been amended
EDIT: There is a small error with my solution when looking to the case that at least 2 of x,y,z are negative, it has been amended
Last edited:



