-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2014 MX2 Marathon (archive) (2 Viewers)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
mathsbrain
Member
- Joined
- Jul 16, 2012
- Messages
- 161
- Gender
- Male
- HSC
- N/A
Last edited:
mathsbrain
Member
- Joined
- Jul 16, 2012
- Messages
- 161
- Gender
- Male
- HSC
- N/A
Re: HSC 2014 4U Marathon
Without letting z=x+iy, explain why the locus of-arg(z-2+2i)=\frac{\pi}{3}) is the major arc of a circle. Find the centre of this circle without letting z=x+iy.
is the major arc of a circle. Find the centre of this circle without letting z=x+iy.
Without letting z=x+iy, explain why the locus of
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon
)-arg(z-(2-2i))=\frac{\pi}{3})
?
---------

Do you meanWithout letting z=x+iy, explain why the locus ofis the major arc of a circle. Find the centre of this circle without letting z=x+iy.
?
---------
mathsbrain
Member
- Joined
- Jul 16, 2012
- Messages
- 161
- Gender
- Male
- HSC
- N/A
Re: HSC 2014 4U Marathon
Do you mean
?
Yes thats exactly what i mean, thanks and i have edited the question now.
aDimitri
i'm the cook
Re: HSC 2014 4U Marathon
Am i allowed to simultaneously solve
-arg(z-2+2i)=\frac{2\pi}{3} \\ |z-3-4i| = |z-2+2i|)
Thus finding the equation of the circle?
ok i'm not 100% sure what constitutes letting z = x+iyWithout letting z=x+iy, explain why the locus ofis the major arc of a circle. Find the centre of this circle without letting z=x+iy.
Am i allowed to simultaneously solve
Thus finding the equation of the circle?
mathsbrain
Member
- Joined
- Jul 16, 2012
- Messages
- 161
- Gender
- Male
- HSC
- N/A
Re: HSC 2014 4U Marathon
We're looking for a geometrical approach without using algebra. So no solving equations(at least not simultaneous equations) if that makes senseok i'm not 100% sure what constitutes letting z = x+iy
Am i allowed to simultaneously solve
Thus finding the equation of the circle?
mathsbrain
Member
- Joined
- Jul 16, 2012
- Messages
- 161
- Gender
- Male
- HSC
- N/A
Re: HSC 2014 4U Marathon
Go http://community.boredofstudies.org/14/mathematics-extension-2/243515/complex-locus-help.htmlHey guys how do i do this
Draw diagram of
Argz[z-(root3+i)] =pie/6
Re: HSC 2014 4U Marathon
sec(x)+tan(x)=A
1/(1-sin(x)) = A
sin(x) = 1 - 1/A
cos^2(x) = 1 - (1-(1/A))^2 = (2A-1)/A^2
cos(x) = ±[sqrt(2A-1)]/A
1/(1 - cos(x)) = A/(A±sqrt(2A-1))
Therefore, cosec(x) + cot(x) = A/(A±sqrt(2A-1)) where A>= 1/2
sec(x)+tan(x)=A
1/(1-sin(x)) = A
sin(x) = 1 - 1/A
cos^2(x) = 1 - (1-(1/A))^2 = (2A-1)/A^2
cos(x) = ±[sqrt(2A-1)]/A
1/(1 - cos(x)) = A/(A±sqrt(2A-1))
Therefore, cosec(x) + cot(x) = A/(A±sqrt(2A-1)) where A>= 1/2
aDimitri
i'm the cook
Re: HSC 2014 4U Marathon
could prove this with co-ordinate geometry but i cbb
is it sufficient to consider the construction of perpendicular bisectors of each of the sides of the triangle formed by the 3 points, and noting that for any 3 points, the 3 perpendicular bisectors all meet at one location, meaning there is only one possible center for a circle touching these three points.
could prove this with co-ordinate geometry but i cbb
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon
Here is a hint:
The general equation of a circle in the co-ordinate plane is: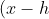^2 + (x-k)^2 = r^2 )
What you are talking about is the orthocenter, but the orthocenter is not the centroid of a triangle and is not equidistant to all 3 points.is it sufficient to consider the construction of perpendicular bisectors of each of the sides of the triangle formed by the 3 points, and noting that for any 3 points, the 3 perpendicular bisectors all meet at one location, meaning there is only one possible center for a circle touching these three points.
could prove this with co-ordinate geometry but i cbb
Here is a hint:
The general equation of a circle in the co-ordinate plane is:
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon
Think about it this way. Lying on a perpendicular bisector of a side means you are equidistant from a certain two of the triangles vertices. So lying on all three perpendicular bisectors means you are equidistant from all three.
(And the centroid is something different altogether. That is the meeting point of the bisecting cevians.)
I think Dimitri is correct. The orthocenter is the intersection of the perpendicular cevians, the intersection of perpendicular bisectors is the circumcenter...which is what your question is asking for.What you are talking about is the orthocenter, but the orthocenter is not the centroid of a triangle and is not equidistant to all 3 points.
Here is a hint:
The general equation of a circle in the co-ordinate plane is: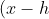^2 + (x-k)^2 = r^2 )
Think about it this way. Lying on a perpendicular bisector of a side means you are equidistant from a certain two of the triangles vertices. So lying on all three perpendicular bisectors means you are equidistant from all three.
(And the centroid is something different altogether. That is the meeting point of the bisecting cevians.)
Last edited:
aDimitri
i'm the cook
Re: HSC 2014 4U Marathon
Don't the perpendicular bisectors meet at the circumcenter?
Yes this is exactly what i meant.I think Dimitri is correct. The orthocenter is the intersection of the perpendicular cevians, the intersection of perpendicular bisectors is the circumcenter...which is what your question is asking for.
Think about it this way. Lying on a perpendicular bisector of a side means you are equidistant from a certain two of the triangles vertices. So lying on all three perpendicular bisectors means you are equidistant from all three.
(And the centroid is something different altogether. That is the meeting point of the bisecting cevians.)
Don't the perpendicular bisectors meet at the circumcenter?
Stygian
Active Member
- Joined
- Aug 11, 2014
- Messages
- 117
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2014 4U Marathon
(interesting to note is that this occurs irrespective of whether this circumcentre is external to the triangle or not)
In terms of what Sy said, the orthocentre is slightly different, it being the intersection of the altitudes of a triangle
your proof is more elegant and yes the the perpendicular bisectors do meet at the circumcentreis it sufficient to consider the construction of perpendicular bisectors of each of the sides of the triangle formed by the 3 points, and noting that for any 3 points, the 3 perpendicular bisectors all meet at one location, meaning there is only one possible center for a circle touching these three points.
could prove this with co-ordinate geometry but i cbb
(interesting to note is that this occurs irrespective of whether this circumcentre is external to the triangle or not)
In terms of what Sy said, the orthocentre is slightly different, it being the intersection of the altitudes of a triangle
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon
I think Dimitri is correct. The orthocenter is the intersection of the perpendicular cevians, the intersection of perpendicular bisectors is the circumcenter...which is what your question is asking for.
Think about it this way. Lying on a perpendicular bisector of a side means you are equidistant from a certain two of the triangles vertices. So lying on all three perpendicular bisectors means you are equidistant from all three.
(And the centroid is something different altogether. That is the meeting point of the bisecting cevians.)
Yes this is exactly what i meant.
Don't the perpendicular bisectors meet at the circumcenter?
Ah I see, ok, my badyour proof is more elegant and yes the the perpendicular bisectors do meet at the circumcentre
(interesting to note is that this occurs irrespective of whether this circumcentre is external to the triangle or not)
In terms of what Sy said, the orthocentre is slightly different, it being the intersection of the altitudes of a triangle
- Status
- Not open for further replies.

