Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
does the cube have to have all those colours at once ?NEXT QUESTION
Each of a set of equal cubes has its six faces painted red, orange, yellow, green, blue and white respectively so that no two cubes are alike and every arrangement of colours is used. How many cubes are there in the set?
Re: HSC 2015 4U Marathon
Yes, a different colour for each face.does the cube have to have all those colours at once ?
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
So every cube has to have every colourYes, a different colour for each face.
Re: HSC 2015 4U Marathon
YesSo every cube has to have every colour
dan964
what
Re: HSC 2015 4U Marathon
my guess
(1) One side will always be painted white, so it is irrelevant what side this is.
(2) We pick now the colour OPPOSITE the white side, as this will also be unique with rotation = 5
(3) And then we rearrange the remaining colours without repetition, which is 3! (we consider it as a circle, so not 4!)
5*3! gives 30.
method 2 is to pick the 4 colours excluding the ends which is 6C4
and then arrange the remaining two colours (which is 2!)
my guess
(1) One side will always be painted white, so it is irrelevant what side this is.
(2) We pick now the colour OPPOSITE the white side, as this will also be unique with rotation = 5
(3) And then we rearrange the remaining colours without repetition, which is 3! (we consider it as a circle, so not 4!)
5*3! gives 30.
method 2 is to pick the 4 colours excluding the ends which is 6C4
and then arrange the remaining two colours (which is 2!)
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
Have no idea for this one tbh
Have no idea for this one tbh
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
Tried to make a question again:



Tried to make a question again:
Re: HSC 2015 4U Marathon
Then use sum of roots for the given equation, divided by sum of roots for the new formed equation, it'll be 1, since when you reverse the coefficients of the given polynomial equation, the coefficients of and
and 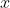 remain unchanged.
remain unchanged.
Form a quartic equation with roots that are reciprocals of those for the given equation (when you do this, the coefficients get "reversed", you'll see).Tried to make a question again:

Then use sum of roots for the given equation, divided by sum of roots for the new formed equation, it'll be 1, since when you reverse the coefficients of the given polynomial equation, the coefficients of
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
DAMNNNNNN i didnt do it that way but thats geniusForm a quartic equation with roots that are reciprocals of those for the given equation (when you do this, the coefficients get "reversed", you'll see).
Then use sum of roots for the given equation, divided by sum of roots for the new formed equation, it'll be 1, since when you reverse the coefficients of the given polynomial equation, the coefficients ofand
remain unchanged.
dan964
what
Re: HSC 2015 4U Marathon
 from product of roots
from product of roots
Anyway next question.
 + cis (2x) + cis (3x) + cis (4x) + ... )
 + sin (2x) + sin (3x) + sin (4x)+ ... )
You do realise thatTried to make a question again:

Anyway next question.
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon

 )
 )
Coded on my phone
Im suppose to say "without using"You do realise thatfrom product of roots
Anyway next question.
 + sin (2x) + sin (3x) + sin (4x)+ ... )
Coded on my phone
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
I think i may have used the wrong formulaIm suppose to say "without using"
Coded on my phone
Last edited:
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,614
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
 + cis(2x) + cis(3x)+... = cis(x) + (cis(x))^2 + (cis(x))^3+... )

And for the next part just find the imaginary bit by realizing the denominator, which should be:
 - 2\sin(x)\times\cos(x)}{2 - 2\cos(x)} )
You do realise thatfrom product of roots
Anyway next question.
 + sin (2x) + sin (3x) + sin (4x)+ ... )
And for the next part just find the imaginary bit by realizing the denominator, which should be:
Last edited:
Re: HSC 2015 4U Marathon
That is ... r must be REAL (To use that formula anyway)
This has no limiting sum.
If x is a rational multiple of pi, the partial sums follow a cyclically repeating pattern.
If x is a non-rational multiple of pi, there is no repeating pattern, but it certainly doesn't converge to a limit.
To have a limiting sum, the MODULUS of successive terms would at the very least have be reducing.
And sin x + sin 2x + sin3x + ... most definitely does not have a limiting sum. ( Except for the trivial case x = k pi )
The restriction for the limiting sum of a GP is r must lie between -1 and 1.
And for the next part just find the imaginary bit by realizing the denominator, which should be:
 - 2\sin(x)\times\cos(x)}{2 - 2\cos(x)} )
That is ... r must be REAL (To use that formula anyway)
This has no limiting sum.
If x is a rational multiple of pi, the partial sums follow a cyclically repeating pattern.
If x is a non-rational multiple of pi, there is no repeating pattern, but it certainly doesn't converge to a limit.
To have a limiting sum, the MODULUS of successive terms would at the very least have be reducing.
And sin x + sin 2x + sin3x + ... most definitely does not have a limiting sum. ( Except for the trivial case x = k pi )
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
x^n) )
(x^n)) )
You do realise thatfrom product of roots
Anyway next question.
 + sin (2x) + sin (3x) + sin (4x)+ ... )
Re: HSC 2015 4U Marathon
So they can't possibly be limiting (ie. infinite) sums.
You have to find limits as n->infinity, and these limits do not exist.
Try x=pi/2:
cisx=i
cisx+cis2x = i - 1
cisx+cis2x+cis3x = i - 1 - i = -1
cisx+cis2x+cis3x+cis4x = i - 1 - i + 1 = 0
And then the cycle repeats - there is NO limit.
Your expressions include an 'n' representing the number of terms.
So they can't possibly be limiting (ie. infinite) sums.
You have to find limits as n->infinity, and these limits do not exist.
Try x=pi/2:
cisx=i
cisx+cis2x = i - 1
cisx+cis2x+cis3x = i - 1 - i = -1
cisx+cis2x+cis3x+cis4x = i - 1 - i + 1 = 0
And then the cycle repeats - there is NO limit.
Last edited:
FrankXie
Active Member
Re: HSC 2015 4U Marathon
a little change would make a good question:

a little change would make a good question:
Last edited:
VBN2470
Well-Known Member
Re: HSC 2015 4U Marathon
x}{2\sin\frac{x}{2}}$. \\ Substituting $x=\frac{\pi}{2015}$ with $n=2014$, and manipulating with our simplified expression, the desired result follows. $ )
EDIT: Not sure if the RHS value is correct, or if I did something wrong and am missing something.
a little change would make a good question:

EDIT: Not sure if the RHS value is correct, or if I did something wrong and am missing something.
Last edited:
- Status
- Not open for further replies.

