HSC 2015 MX2 Marathon (archive) (5 Viewers)

seanieg89 · Feb 12, 2015

Re: HSC 2015 4U Marathon

Yeah, quite sure 30 is correct.

Drsoccerball · Feb 12, 2015

Re: HSC 2015 4U Marathon

FrankXie said:
NEXT QUESTION

Each of a set of equal cubes has its six faces painted red, orange, yellow, green, blue and white respectively so that no two cubes are alike and every arrangement of colours is used. How many cubes are there in the set?

does the cube have to have all those colours at once ?

InteGrand · Feb 12, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
does the cube have to have all those colours at once ?

Yes, a different colour for each face.

Drsoccerball · Feb 12, 2015

Re: HSC 2015 4U Marathon

InteGrand said:
Yes, a different colour for each face.

So every cube has to have every colour

InteGrand · Feb 12, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
So every cube has to have every colour

Yes

dan964 · Feb 12, 2015

Re: HSC 2015 4U Marathon

my guess
(1) One side will always be painted white, so it is irrelevant what side this is.
(2) We pick now the colour OPPOSITE the white side, as this will also be unique with rotation = 5
(3) And then we rearrange the remaining colours without repetition, which is 3! (we consider it as a circle, so not 4!)
5*3! gives 30.

method 2 is to pick the 4 colours excluding the ends which is 6C4
and then arrange the remaining two colours (which is 2!)

Drsoccerball · Feb 12, 2015

Re: HSC 2015 4U Marathon

Have no idea for this one tbh

Drsoccerball · Feb 12, 2015

Re: HSC 2015 4U Marathon

Tried to make a question again:

$$ Given that $ x^4 +\alpha x^3+5\alpha x^2 +\alpha x+1=0 $ has roots $ \alpha , \beta , \gamma , \delta$

$Without letting $ \alpha\beta\gamma\delta=1 $ Prove that$

$\frac{\alpha +\beta +\gamma +\delta}{\frac{1}{\alpha}+ \frac{1}{\beta} + \frac{1}{\gamma} + \frac{1}{\delta}}=1$

InteGrand · Feb 12, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
Tried to make a question again:

$$ Given that $ x^4 +\alpha x^3+5\alpha x^2 +\alpha x+1=0 $ has roots $ \alpha , \beta , \gamma , \delta$

$Without letting $ \alpha\beta\gamma\delta=1 $ Prove that$

$\frac{\alpha +\beta +\gamma +\delta}{\frac{1}{\alpha}+ \frac{1}{\beta} + \frac{1}{\gamma} + \frac{1}{\delta}}=1$

Form a quartic equation with roots that are reciprocals of those for the given equation (when you do this, the coefficients get "reversed", you'll see).

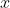Then use sum of roots for the given equation, divided by sum of roots for the new formed equation, it'll be 1, since when you reverse the coefficients of the given polynomial equation, the coefficients of $x^3$ and $x$ remain unchanged.

Drsoccerball · Feb 12, 2015

Re: HSC 2015 4U Marathon

InteGrand said:
Form a quartic equation with roots that are reciprocals of those for the given equation (when you do this, the coefficients get "reversed", you'll see).

Then use sum of roots for the given equation, divided by sum of roots for the new formed equation, it'll be 1, since when you reverse the coefficients of the given polynomial equation, the coefficients of $x^3$ and $x$ remain unchanged.

DAMNNNNNN i didnt do it that way but thats genius

dan964 · Feb 12, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
Tried to make a question again:

$$ Given that $ x^4 +\alpha x^3+5\alpha x^2 +\alpha x+1=0 $ has roots $ \alpha , \beta , \gamma , \delta$

$Without letting $ \alpha\beta\gamma\delta=1 $ Prove that$

$\frac{\alpha +\beta +\gamma +\delta}{\frac{1}{\alpha}+ \frac{1}{\beta} + \frac{1}{\gamma} + \frac{1}{\delta}}=1$

You do realise that $$ \alpha\beta\gamma\delta=1$ from product of roots
Anyway next question.

$$ Find the limiting sum of $ cis (x) + cis (2x) + cis (3x) + cis (4x) + ...$
$$ and hence simplify $ sin (x) + sin (2x) + sin (3x) + sin (4x)+ ...$

Drsoccerball · Feb 12, 2015

Re: HSC 2015 4U Marathon

dan964 said:
You do realise that $$ \alpha\beta\gamma\delta=1$ from product of roots
Anyway next question.

$$ Find the limiting sum of $ cis (x) + cis (2x) + cis (3x) + cis (4x) + ...$
$$ and hence simplify $ sin (x) + sin (2x) + sin (3x) + sin (4x)+ ...$

Im suppose to say "without using"

$cisx +cis2x+...$

$= cis(\frac{x}{1-x})$

$\therefore sinx +sin2x+...=sin(\frac{x}{1-x})$

Coded on my phone

Drsoccerball · Feb 12, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
Im suppose to say "without using"

$cisx +cis2x+...$

$= cis(\frac{x}{1-x})$

$\therefore sinx +sin2x+...=sin(\frac{x}{1-x})$

Coded on my phone

I think i may have used the wrong formula

braintic · Feb 12, 2015

Re: HSC 2015 4U Marathon

dan964 said:
$$ Find the limiting sum of $ cis (x) + cis (2x) + cis (3x) + cis (4x) + ...$
$$ and hence simplify $ sin (x) + sin (2x) + sin (3x) + sin (4x)+ ...$

Surely this won't have a limiting sum.

Ekman · Feb 12, 2015

Re: HSC 2015 4U Marathon

dan964 said:
You do realise that $$ \alpha\beta\gamma\delta=1$ from product of roots
Anyway next question.

$$ Find the limiting sum of $ cis (x) + cis (2x) + cis (3x) + cis (4x) + ...$
$$ and hence simplify $ sin (x) + sin (2x) + sin (3x) + sin (4x)+ ...$

$cis(x) + cis(2x) + cis(3x)+... = cis(x) + (cis(x))^2 + (cis(x))^3+...$

$\therefore $ limiting sum is: $ \frac{cisx}{1-cisx}$

And for the next part just find the imaginary bit by realizing the denominator, which should be:

$\frac{\sin(x) - 2\sin(x)\times\cos(x)}{2 - 2\cos(x)}$

braintic · Feb 12, 2015

Re: HSC 2015 4U Marathon

Ekman said:
$cis(x) + cis(2x) + cis(3x)+... = cis(x) + (cis(x))^2 + (cis(x))^3+...$

$\therefore $limiting sum is: $ \frac{cisx}{1-cisx}$

And for the next part just find the imaginary bit by realizing the denominator, which should be:

$\frac{\sin(x) - 2\sin(x)\times\cos(x)}{2 - 2\cos(x)}$

The restriction for the limiting sum of a GP is r must lie between -1 and 1.

That is ... r must be REAL (To use that formula anyway)

This has no limiting sum.
If x is a rational multiple of pi, the partial sums follow a cyclically repeating pattern.
If x is a non-rational multiple of pi, there is no repeating pattern, but it certainly doesn't converge to a limit.

To have a limiting sum, the MODULUS of successive terms would at the very least have be reducing.

And sin x + sin 2x + sin3x + ... most definitely does not have a limiting sum. ( Except for the trivial case x = k pi )

Drsoccerball · Feb 12, 2015

Re: HSC 2015 4U Marathon

dan964 said:
You do realise that $$ \alpha\beta\gamma\delta=1$ from product of roots
Anyway next question.

$$ Find the limiting sum of $ cis (x) + cis (2x) + cis (3x) + cis (4x) + ...$
$$ and hence simplify $ sin (x) + sin (2x) + sin (3x) + sin (4x)+ ...$

$cis((n!)x^n)$

$\therefore sinx +sin2x...=sin((n!)(x^n))$

braintic · Feb 12, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
$cis((n!)x^n)$

$\therefore sinx +sin2x...=sin((n!)(x^n))$

Your expressions include an 'n' representing the number of terms.
So they can't possibly be limiting (ie. infinite) sums.

You have to find limits as n->infinity, and these limits do not exist.

Try x=pi/2:

cisx=i
cisx+cis2x = i - 1
cisx+cis2x+cis3x = i - 1 - i = -1
cisx+cis2x+cis3x+cis4x = i - 1 - i + 1 = 0
And then the cycle repeats - there is NO limit.

FrankXie · Feb 12, 2015

Re: HSC 2015 4U Marathon

a little change would make a good question:

$$ Simplify $ \sin{x}+\sin2x+\sin3x+\cdots+\sin{nx}. $ Hence show that $ \sin\frac{\pi}{2015}+\sin\frac{2\pi}{2015}+ \sin \frac{3\pi}{2015}+\cdots+\sin\frac{\2014\pi}{2015}= \cot\frac{\pi}{4030}.$

VBN2470 · Feb 12, 2015

Re: HSC 2015 4U Marathon

FrankXie said:
a little change would make a good question:

$$ Simplify $ \sin{x}+\sin2x+\sin3x+\cdots+\sin{nx}. $ Hence show that $ \sin\frac{\pi}{2015}+\sin\frac{2\pi}{2015}+ \sin \frac{3\pi}{2015}+\cdots+\sin\frac{\2014\pi}{2015}= \cot\frac{\pi}{3030}.$

$Simplified expression is $\frac{\cos\frac{x}{2}-\cos(n+\frac{1}{2})x}{2\sin\frac{x}{2}}$. \\ Substituting $x=\frac{\pi}{2015}$ with $n=2014$, and manipulating with our simplified expression, the desired result follows.$

EDIT: Not sure if the RHS value is correct, or if I did something wrong and am missing something.

HSC 2015 MX2 Marathon (archive) (5 Viewers)

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

what

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

what

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Active Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 5)