-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon
That wasn't what I did but that may workI'm assuming you would use a similar method but instead of using the numbers F_n, you would use the factors of those integers, and prove that the factors cannot be integers, hence proving they do not share common factors.
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon
It's a little unclear what you are saying in the middle but I see what you are trying to say, it is my method too


a^2 - b^2 [/tex]
Not sure if this is valid?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon
I'm getting a lot of these questions from:
http://mathsorchard.weebly.com/step-past-papers.html
http://www.physicsandmathstutor.com/step/
STEP papers are very valuable resources for MX2 since the questions are of advanced difficulty (relative to the HSC) and are of HSC style. Though there may be some topics outside the syllabus in these papers, if you're able to spot them and avoid them, then otherwise the questions are great (and sometimes the HSC and companies like CSSA rip questions out of these!)
I'm getting a lot of these questions from:
http://mathsorchard.weebly.com/step-past-papers.html
http://www.physicsandmathstutor.com/step/
STEP papers are very valuable resources for MX2 since the questions are of advanced difficulty (relative to the HSC) and are of HSC style. Though there may be some topics outside the syllabus in these papers, if you're able to spot them and avoid them, then otherwise the questions are great (and sometimes the HSC and companies like CSSA rip questions out of these!)
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,611
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
Isn't this exactly the same as the previous question? Instead that you say pq is an odd number, because prime numbers greater than 2 are odd numbers, and so the only two way they can be written in the form of a^2 - b^2 is when a is odd and b is even and vice versa. However you cant write pq like that if either p or q is 2 as an even number multiplied by anything results in an even number.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon
Can you expand on your method? From what I can see you've proven that there are 2 possibilities, for a, b (that a is even b odd, a odd b even) but that doesn't mean there are exactly 2 solutions, for example 675 can be written in (i think it's 6) different ways of having a^2 - b^2, even though there are only 2 possibilities.Isn't this exactly the same as the previous question? Instead that you say pq is an odd number, because prime numbers greater than 2 are odd numbers, and so the only two way they can be written in the form of a^2 - b^2 is when a is odd and b is even and vice versa. However you cant write pq like that if either p or q is 2 as an even number multiplied by anything results in an even number.
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 661
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
https://imgur.com/kldJ69o
Here's my solution for part (i) and an idea for part (ii) - it's probably not written in the most mathematically concise way but it's something:
https://imgur.com/kldJ69o
SilentWaters
Member
- Joined
- Mar 20, 2014
- Messages
- 55
- Gender
- Male
- HSC
- 2014
Re: HSC 2015 4U Marathon
Perhaps a more systematic variation of your response would mention two things:
(1) the quadratic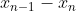 is monotonically increasing above zero for x > 3, meaning that successive values of x starting from 4 get larger and larger. That is, we continue to move right along that quadratic with each new iteration of x from
is monotonically increasing above zero for x > 3, meaning that successive values of x starting from 4 get larger and larger. That is, we continue to move right along that quadratic with each new iteration of x from 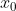 , guaranteeing the inequality in (i)
, guaranteeing the inequality in (i)
(2) in the range 2 < x < 3 the inequality breaks down, sure, but what about x = 2 and x < 2? Mention that the inequality turns into an equality for the former case, and in the latter case, the quadratic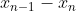 (the difference between successive values of x) monotonically decreases towards zero. That is,
(the difference between successive values of x) monotonically decreases towards zero. That is,  as
as  , until we again have an equality instead of an inequality.
, until we again have an equality instead of an inequality.
Perhaps a more systematic variation of your response would mention two things:
(1) the quadratic
(2) in the range 2 < x < 3 the inequality breaks down, sure, but what about x = 2 and x < 2? Mention that the inequality turns into an equality for the former case, and in the latter case, the quadratic
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon

It might be a misinterpretation but it seems you assume that x(0) is the lowest of the x(n) which from there allows you to prove that x(n+1) > x(n).
So it is either circular in that you assume x(n+1) > x(n) to get that min(x(n)) = x(0), or, you have independent reasons for knowing that min(x(n)) = x(0), in which case what would you say to prove this?
What if because of the 1/5 in front of the bracket that there is some value below x(0)?
The general gist of it is true however (the reasoning prior to this), and to complete the proof safely, I would recommend simply using proof by induction
Step 1 is easy, since we can calculate x(1) and show that x(1) > x(0).
Step 2 allows us the assumption that x(k) > x(k-1) > ... > x(0) = 4 > 3
Step 3, the inductive step, simply requires doing what you've already done, but then using Step 2 as justification for x(n) > x(0).
------
As for part 2, it is sufficient to show that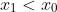 for
for 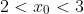
I may be wrong but I feel like there is some sort of circularity here:Here's my solution for part (i) and an idea for part (ii) - it's probably not written in the most mathematically concise way but it's something:
https://imgur.com/kldJ69o

It might be a misinterpretation but it seems you assume that x(0) is the lowest of the x(n) which from there allows you to prove that x(n+1) > x(n).
So it is either circular in that you assume x(n+1) > x(n) to get that min(x(n)) = x(0), or, you have independent reasons for knowing that min(x(n)) = x(0), in which case what would you say to prove this?
What if because of the 1/5 in front of the bracket that there is some value below x(0)?
The general gist of it is true however (the reasoning prior to this), and to complete the proof safely, I would recommend simply using proof by induction
Step 1 is easy, since we can calculate x(1) and show that x(1) > x(0).
Step 2 allows us the assumption that x(k) > x(k-1) > ... > x(0) = 4 > 3
Step 3, the inductive step, simply requires doing what you've already done, but then using Step 2 as justification for x(n) > x(0).
------
As for part 2, it is sufficient to show that
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,611
- Gender
- Male
- HSC
- 2015
Axio
=o
- Joined
- Mar 20, 2014
- Messages
- 483
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
a=kvx
dv/dx =kx
integrating gives: v=k/2(x^2 + d^2)
v=dx/dt
integrating gives: x=dtan((2dkt+pi)/4)
as x->inf, (2dkt+pi)/4 -> pi/2. And rearranging gives required result
ii.
x=sqrt((U^2 -B^2)/e^-kt/B -1) +U^2), where B=d^2 -2U/k
as t->inf, x->d^2-2U/k
i.
a=kvx
dv/dx =kx
integrating gives: v=k/2(x^2 + d^2)
v=dx/dt
integrating gives: x=dtan((2dkt+pi)/4)
as x->inf, (2dkt+pi)/4 -> pi/2. And rearranging gives required result
ii.
x=sqrt((U^2 -B^2)/e^-kt/B -1) +U^2), where B=d^2 -2U/k
as t->inf, x->d^2-2U/k
Last edited:
- Status
- Not open for further replies.


