Re: HSC 2015 4U Marathon
We will prove existence and uniqueness separately.
Existence we do inductively.
It is trivial for n=1.
Now suppose that there exist positive integers
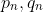
such that
^n=p_n+q_n\sqrt{2}.)
Then
^{n+1}=(1+\sqrt{2})(p_n+\q_n\sqrt{2})=(p_n+2q_n)+(p_n+q_n)\sqrt{2}=p_{n+1}+q_{n+1}\sqrt{2}.)
The coefficients clearly being positive integers.
Uniqueness follows from the fact that we cannot write the same real number in more than one way in this form.
For if we have
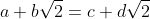
and
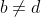
(if b=d then we can subtract the surdic terms and also get a=b), then
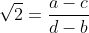
, which contradicts the well-known fact that
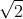
is irrational. (I can prove this if you like, but I think most people have seen it before.)
Proving that
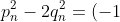^n)
is done inductively, as
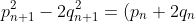^2-2(p_n+q_n)^2=-(p_n^2-2q_n^2)=(-1)^{n+1}.)
An interesting extension question (more suitable for the advanced thread) is to show that:
a) There are always positive integer solutions to the equation
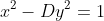
if D is a nonsquare positive integer. (Hint: use the pigeonhole principle and consider the problem of approximating an irrational number well by a rational one.)
b) The solutions are precisely the pairs
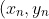)
where (
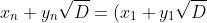^n)
) and
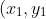)
is the solution pair with smallest
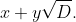
(Hint: again consider multiplying numbers of the form
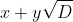
together.)
c) Find a closed form (non-recursive) expression for the solutions.
(If a is too hard, then just try b and c, as they are a bit easier I reckon.)
, what happens when
?


