davidgoes4wce
Well-Known Member
My initial think was 0.25% as well
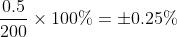
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
How reliable are the answers of the question's source?My initial think was 0.25% as well
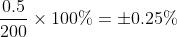
But you said the answer was D) – is this reliable?There are no answers, just ticks and crosses.
No solutions given to student.
Yeah it appears that these markings are quite unreliable.The teacher who marked it on the MCQ gave Q14 D (was deemed wrong), Q15 D (was deemed correct)
Im skeptical because when I did Q 14 :
Which was marked wrong.
Wouldn't the students have complained if there were so many blatant errors?This school has fckued up their students , they have done Question 16 wrong as well.
The student that I am tutoring wasn't good enough , he failed the General Maths exam. I don't think he would have been able to spot the errors out and he left half of the short answer section.Wouldn't the students have complained if there were so many blatant errors?
Which answer was marked correct here?
Yeah it should be B) (Simpson's Rule).
My answer would have been B, the answer that was marked correct was D


