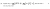HSC Mathematics Marathon (1 Viewer)

math man · Oct 20, 2011

largarithmic said:
Yeah I know what the MVT is, but I don't really get how your proof of seanieg89's question actually works (like how do you assume f'(c) is constant , presumably as you range x and y)

if f(x) is my function then f'(x) is my derivative, so subbing c into the derivative, i.e f'(c), will give me a constant

hup · Oct 20, 2011

$I_n=\int_{1}^{e}(1-\ln x)^n \ dx\ for\ n\geq0\\\\\\\ (i)\ Show\ that\ for\ n\geq 1\ \\\\ I_n=-1+n\ I_{n-1} \\\\ (ii)\ Evaluate\ \frac{I_n}{n!}\ and\ deduce\ that \ \lim_{n \to \infty } \sum_{k=0}^{n}\frac{1}{k!}=e$

you cannot assume that $I_n<n!$

blackops23 · Oct 20, 2011

seanieg89 said:
$$By summing the geometric series we get: \\$\sum_{k=0}^n \cos((2k+1)\theta)=\frac{1}{2}\sum_{k=0}^n z^{2k+1}+z^{-2k-1}=\frac{z^{2n+2}-z^{-2n-2}}{2(z-z^{-1})}=\frac{\sin(2(n+1)\theta)}{2\sin(\theta)}.$

Sorry guys someone please explain this to me, how do you know the series is geometric? havent done much work with series :S

Wight · Oct 21, 2011

hup said:
$I_n=\int_{1}^{e}(1-\ln x)^n \ dx\ for\ n\geq0\\\\\\\ (i)\ Show\ that\ for\ n\geq 1\ \\\\ I_n=-1+n\ I_{n-1} \\\\ (ii)\ Evaluate\ \frac{I_n}{n!}\ and\ deduce\ that \ \lim_{n \to \infty } \sum_{k=0}^{n}\frac{1}{k!}=e$

you cannot assume that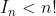 $I_n<n!$

$i) \quad I_{n}=\int_{1}^{e}(1-ln(x))^ndx \newline =[e(1-ln(e))^n]-[1(1-ln(1))^n] - \int_{1}^{e}nx(-\frac{1}{x})(1-ln(x))^ndx \newline =0-1 +nI_{n-1} \newline \newline ii) \quad \frac{I_n}{n!} = \frac{-1+nI_{n-1}}{n!}\newline =\frac{I_{n-1}}{(n-1)!}-\frac{1}{n!}\newline =\frac{I_{n-2}}{(n-2)!}-\frac{1}{(n-1)!}-\frac{1}{n!}\newline =I_0-1-\frac{1}{2!}-\frac{1}{3!}...-\frac{1}{n!}\newline =(e-1)-1...-\frac{1}{n!}\newline =e-(\sum_{k=0}^{n}\frac{1}{k!})\newline \newline\newline because\;I\;can't\;assume,\;I\;shall\;prove\;(excuse\;the\;mess,\;being\;lazy)\newline I_1 = e-2 < 1! \newline assuming\;I_{n}<n!\newline I_{n+1}=-1+(n+1)I_{n}\quad(from\;part\;(i))\newline \therefore I_{n+1}<-1+(n+1)n!\quad(by\;assumption)\newline \therefore I_{n+1}<(n+1)!-1<(n+1)!\newline hence\;valid\;for\;all\;\geq 1\newline\newline \therefore as\;I_n<n!\newline \lim_{n\to\infty}\frac{I_n}{n!}=\lim_{n\to\infty}(e-\sum_{k=0}^{n}\frac{1}{k!}) = 0\newline \therefore \lim_{n\to\infty}\sum_{k=0}^{n}\frac{1}{k!}=e$

now is a solution like this accepted?
I also do not have another question...someone else can put one up.

hup · Oct 21, 2011

Wight said:
$i) \quad I_{n}=\int_{1}^{e}(1-ln(x))^ndx \newline =[e(1-ln(e))^n]-[1(1-ln(1))^n] - \int_{1}^{e}nx(-\frac{1}{x})(1-ln(x))^ndx \newline =0-1 +nI_{n-1} \newline \newline ii) \quad \frac{I_n}{n!} = \frac{-1+nI_{n-1}}{n!}\newline =\frac{I_{n-1}}{(n-1)!}-\frac{1}{n!}\newline =\frac{I_{n-2}}{(n-2)!}-\frac{1}{(n-1)!}-\frac{1}{n!}\newline =I_0-1-\frac{1}{2!}-\frac{1}{3!}...-\frac{1}{n!}\newline =(e-1)-1...-\frac{1}{n!}\newline =e-(\sum_{k=0}^{n}\frac{1}{k!})\newline \newline\newline because\;I\;can't\;assume,\;I\;shall\;prove\;(excuse\;the\;mess,\;being\;lazy)\newline I_1 = e-2 < 1! \newline assuming\;I_{n}<n!\newline I_{n+1}=-1+(n+1)I_{n}\quad(from\;part\;(i))\newline \therefore I_{n+1}<-1+(n+1)n!\quad(by\;assumption)\newline \therefore I_{n+1}<(n+1)!-1<(n+1)!\newline hence\;valid\;for\;all\;\geq 1\newline\newline \therefore as\;I_n<n!\newline \lim_{n\to\infty}\frac{I_n}{n!}=\lim_{n\to\infty}(e-\sum_{k=0}^{n}\frac{1}{k!}) = 0\newline \therefore \lim_{n\to\infty}\sum_{k=0}^{n}\frac{1}{k!}=e$

now is a solution like this accepted?
I also do not have another question...someone else can put one up.

idk if you can use induction like that it's like taking the easy way out

Wight · Oct 21, 2011

yeah neither do I...
also I skip too many steps -.-

Some Vunt · Oct 21, 2011

What's the current question?

hup · Oct 21, 2011

Some Vunt said:
What's the current question?

last part of In one

hup · Oct 21, 2011

start with

$1\leq x\leq e$

Wight · Oct 21, 2011

hup said:
start with

$1\leq x\leq e$

as for $1\leq x\leq e$ then $0\leq 1-ln(x)\leq 1$ .
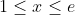
So as any irrational (< 1)^n is even smaller, then as $\lim_{n\to\infty}I_n = 0$ . Apply that to my solution as relevant and it should be good (too lazy to do it again).

Yeah the above will need alot more work to suit a proper solution...just a general idea.

I'm still curious as to whether you can use induction...it's obviously the longer process, but the easier way out when you don't think of the obvious...can anyone clarify?

apollo1 · Oct 21, 2011

question similar to this in 2005 hsc where induction was used.

Wight · Oct 21, 2011

Hmm okay. Personally I don't see why it can't be used...but I guess that's the marker's decision. Not mine.

seanieg89 · Oct 21, 2011

hup · Oct 21, 2011

that is the correct way

seanieg89 · Oct 21, 2011

apollo1 · Oct 21, 2011

seanieg89 said:
$Evaluate the sum:$\\S_n:=1+x\cos(x)+\ldots+x^n\cos(nx)\\$where $x$ is real. A related question that is probably too difficult to be asked in the HSC is: ``For which values of $x$ does this series converge as $n\rightarrow\infty$?''$

can we solve this using hsc knowledge?

hup · Oct 21, 2011

seanieg89 said:
$Evaluate the sum:$\\S_n:=1+x\cos(x)+\ldots+x^n\cos(nx)\\$where $x$ is real. A related question that is probably too difficult to be asked in the HSC is: ``For which values of $x$ does this series converge as $n\rightarrow\infty$?''$

you use the series

S = 1+xcisx+(xcisx)^2+....+(xcisx)^n

then sum it using a gp and equate the real parts

for it to conerge |r| if r is the common ratio must be <1

but since r is xcisx then |r| = x

so x<1 for it to converge?

apollo1 · Oct 21, 2011

can someone help me with this question:

largarithmic · Oct 21, 2011

hup said:
you use the series

S = 1+xcisx+(xcisx)^2+....+(xcisx)^n

then sum it using a gp and equate the real parts

for it to conerge |r| if r is the common ratio must be <1

but since r is xcisx then |r| = x

so x<1 for it to converge?

you mean |x| < 1, negative values of x and zero still work

to make sure the GP converges, do it like this:

$S_n = 1+xcis(x)+x^2cis(2x)+...+x^ncis(nx) = \frac{1 - (xcisx)^n}{1-xcisx}$

So if we let $xcisx = z, S_n = \frac{1-z^n}{1-z}$
which converges as n->infinity if |z| < 1, and diverges if |z|>1. If |z|=1, i.e. x = 1 or -1, it neither converges nor diverges: it just sorta oscillates around the place (although, since 1 is not a rational multiple of pi, its not actually periodic but rather slightly chaotic). Clearly |z| = |x|, so it converges iff |x|<1, goes weird if |x| = 1 and diverges if |x| > 1.

Cool question!

EDIT: oh wait I kinda messed it up because I showed the cis sum diverges, not Re(cissum). Its pretty easy to do that though I think:

$S_n = Re\left(\frac{1-x^n(cos(nx)+isin(nx))}{1-x(cosx+isinx)}\right) = \frac{(1-x^ncos(nx))(1-xcosx)+x^{n+1}sinxsin(nx)}{(1-xcosx)^2+x^2sin^2x} = \frac{1-xcosx+x^n(xcos((n-1)x)-cos(nx))}{1-2xcosx+x^2}$

Now note that as n goes to infinity, the demoninator remains the same while the numerator converges if |x|<1. For |x|>=1, its a lot more complicated but it certainly doesnt converge; it doesnt necessarily "increase without bound though", it sorta oscillates whilst "diverging" at the same time (I dont actually know the technical definition of diverging so yeah, in this case a function like xsinx diverges even though it has zeroes for arbitrarily large x)

seanieg89 · Oct 21, 2011

largarithmic said:
you mean |x| < 1, negative values of x and zero still work

to make sure the GP converges, do it like this:

$S_n = 1+xcis(x)+x^2cis(2x)+...+x^ncis(nx) = \frac{1 - (xcisx)^n}{1-xcisx}$

So if we let $xcisx = z, S_n = \frac{1-z^n}{1-z}$
which converges as n->infinity if |z| < 1, and diverges if |z|>1. If |z|=1, i.e. x = 1 or -1, it neither converges nor diverges: it just sorta oscillates around the place (although, since 1 is not a rational multiple of pi, its not actually periodic but rather slightly chaotic). Clearly |z| = |x|, so it converges iff |x|<1, goes weird if |x| = 1 and diverges if |x| > 1.

Cool question!

Exactly, and your mention of the chaotic nature of the partial sums for certain x brings up an interesting point...consider the same problem if you replace the series by:

$\sum_{k=1}^n\frac{\sin(kx)}{k}$

(Considerably harder than the geometric series case)

HSC Mathematics Marathon (1 Viewer)

Member

Member

Member

ಠ_ಠ

Member

ಠ_ಠ

Banned

Member

Member

ಠ_ಠ

Banned

ಠ_ಠ

Well-Known Member

Member

Well-Known Member

Banned

Member

Banned

Attachments

Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)