I wrote the set of solutions that you are referring to here.
As for Q12a), I think NESA should accept both solutions. A slope field is not sufficient to define the equation of a line passing through a point as there is not enough detail on the slope field to accurately plot it. I can see why it could be either, and I have seen several solutions of it going up and down from both teachers and students. I'm kinda on the fence about this question, I think it was a bad question from NESA and they should have just provided one with a more clear-cut answer as I don't see what is being assessed if NESA decides to lean a certain way.
For Q12b), I have mimicked a solution from the Cambridge textbook (page 582 of Extension 1 textbook) which redefines the variable A from positive only to non-zero as a result of removing the absolute value. This is why I wrote "now the domain of A is A=/=0", since previously it was A>0. The Cambridge solutions does something similar, writing that "A is positive" and upon removing the absolute value, "A is positive or negative". To be more precise, I should have redefined a new variable B and have said that
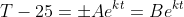
for B=/=0 which I have now done in an updated set of solutions.
For Q12c), there isn't really a need to write integers since n has already been defined to be an integer. This was seen in the 2020 Extension 1 solutions and was also extensively discussed on the 2005 Extension 2 solutions, which said that concluding statements of many students were too long and suggested writing "Hence the statement is true for all n>=0 by induction". I have told students whose teachers were pedantic with concluding statements to refer to official solutions as teachers cannot refute a three paragraph discussion and recommendation by an official set of solutions.
For Q13b), I would doubt they'd need that much justification since the displacement equation assumes there are no walls or floor, and so a simple line stating that if it lands partway up the wall, then it couldn't have touched the floor would have been sufficient. This is kind of obvious since if it touches the floor then the height is less than or equal to zero.
For Q14a), I think this was just a terrible question. They should have explained to use a vector method, or they should have had defined it using vectors. The vector method for this question is inefficient (as numerous students who used this method have pointed out) and the sine rule is the only good way to do it. Regardless, NESA cannot refuse marks for alternative methods as I have emailed them about this issue and they have responded with
"The syllabus does not specify any specific method that students must use to solve problems. HSC markers are aware of alternative methods. Students will not be assessed on the method used but on the correct results of the process."
This opens the door for unorthodox methods and out of syllabus methods. However, I usually recommend against out of syllabus methods since nobody knows how you will be marked and whether you need to prove out of syllabus results before using.
