Jmmalic220
New Member
- Joined
- Mar 8, 2016
- Messages
- 9
- Gender
- Male
- HSC
- 2017
How should we work out these questions?
Q 16
A half-pipe is to be made from a rectangular piece of metal of length x meters. The perimeter of the rectangle is 30 meters.

(a) Find the derivatives of the rectangle that will give the maximum surface area, correct to 1 decimal place. [Answer: 7.5]
(b) Find the height from the ground up to the top of the half-pipe with this maximum area, correct to 1 decimal place. [Answer: 2.4]
Q 18
The picture frame shown below has a border of 2 cm at the top and bottom and 3 cm at the sides. If the total area of the border is to be 100 cm2, find the maximum area of the frame. [Answer: 160 1/6 cm2)
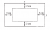
Q 21
X is a point on the curve y=x2-2x+5. Point Y lies directly below X and is on the curve y = 4x-x2. The distance d between X and Y is given by d=2x2-6x+5.
(b) Find the minimum distance between X and Y. [Answer: 1/2 unit]
Q 24
Grant is at point A on one side of a 20 m wide river and needs to get to point B on the other side 80 m along the bank as shown.

Grant swims to any point on the other bank and then runs along the side of the river to point B. If he can swim at 7 km/h and run at 11 km/h, find the distance he swims (x) to minimise the time taken to reach point B. Answer to the nearest metre. [Answer: 26 m]
Q 25
A truck travels 1500 km at an hourly cost given by s2 + 9000 cents where s is the average speed of the truck.
The cost for the trip is given by C = 1500(s+(9000/s)).
(b) Find the speed that minimises the cost of the trip. [Answer: 95 km/h]
(c) Find the cost of the trip to the nearest dollar. [Answer: $2846]
Q 16
A half-pipe is to be made from a rectangular piece of metal of length x meters. The perimeter of the rectangle is 30 meters.

(a) Find the derivatives of the rectangle that will give the maximum surface area, correct to 1 decimal place. [Answer: 7.5]
(b) Find the height from the ground up to the top of the half-pipe with this maximum area, correct to 1 decimal place. [Answer: 2.4]
Q 18
The picture frame shown below has a border of 2 cm at the top and bottom and 3 cm at the sides. If the total area of the border is to be 100 cm2, find the maximum area of the frame. [Answer: 160 1/6 cm2)

Q 21
X is a point on the curve y=x2-2x+5. Point Y lies directly below X and is on the curve y = 4x-x2. The distance d between X and Y is given by d=2x2-6x+5.

(b) Find the minimum distance between X and Y. [Answer: 1/2 unit]
Q 24
Grant is at point A on one side of a 20 m wide river and needs to get to point B on the other side 80 m along the bank as shown.

Grant swims to any point on the other bank and then runs along the side of the river to point B. If he can swim at 7 km/h and run at 11 km/h, find the distance he swims (x) to minimise the time taken to reach point B. Answer to the nearest metre. [Answer: 26 m]
Q 25
A truck travels 1500 km at an hourly cost given by s2 + 9000 cents where s is the average speed of the truck.
The cost for the trip is given by C = 1500(s+(9000/s)).
(b) Find the speed that minimises the cost of the trip. [Answer: 95 km/h]
(c) Find the cost of the trip to the nearest dollar. [Answer: $2846]
Last edited:
