-
Coming soon...BoS Trial exams Announcement imminent!
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
MX2 Marathon (3 Viewers)
- Thread starter dan964
- Start date
xoNat
don't worry, be happy
- Joined
- Apr 30, 2022
- Messages
- 1,467
- Gender
- Undisclosed
- HSC
- 2024
Compound angle formulas, they're on the reference sheetQuestion:
How did they get from this step to the other step shown below? I feel like i'm missing smthn pretty obvious
View attachment 41860
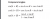
scaryshark09
∞∆ who let 'em cook dis long ∆∞
- Joined
- Oct 20, 2022
- Messages
- 1,591
- Gender
- Undisclosed
- HSC
- 1999
for the first one, i think its meant to be x^2, instead of 2^x
all they do is split up the 2x into x+x and then they rearrange the algebra for the first step
all they do is split up the 2x into x+x and then they rearrange the algebra for the first step
- Joined
- Aug 29, 2021
- Messages
- 1,516
- Gender
- Male
- HSC
- 2024
Ahh makes sense. I was wondering abt that.for the first one, i think its meant to be x^2, instead of 2^x
all they do is split up the 2x into x+x and then they rearrange the algebra for the first step
scaryshark09
∞∆ who let 'em cook dis long ∆∞
- Joined
- Oct 20, 2022
- Messages
- 1,591
- Gender
- Undisclosed
- HSC
- 1999
for the second one they are just factorising, but i think its meant to be xm instead of just x
scaryshark09
∞∆ who let 'em cook dis long ∆∞
- Joined
- Oct 20, 2022
- Messages
- 1,591
- Gender
- Undisclosed
- HSC
- 1999
and again its meant to be x^2, not 2^xfor the second one they are just factorising, but i think its meant to be xm instead of just x
- Joined
- Aug 29, 2021
- Messages
- 1,516
- Gender
- Male
- HSC
- 2024
Fair enough. Just some bad working out answers igfor the second one they are just factorising, but i think its meant to be xm instead of just x
e^(-pi/2i) is just 1cis(-pi/2) which is -i, then multiplying that by -2i is pretty simpleHave I been smoking crack or what is this View attachment 42150
Average Boreduser
Rising Renewal
convert e^...sdjkjfhwkjehgkle to cis form and the i is basically xing cispi/2?Have I been smoking crack or what is this View attachment 42150
Last edited:
- Joined
- Aug 29, 2021
- Messages
- 1,516
- Gender
- Male
- HSC
- 2024
In the end it was just cuz I didn't know eulers formulaOr...
Or...
Cool... I was just showing some other approachesIn the end it was just cuz I didn't know eulers formula
- Joined
- Aug 29, 2021
- Messages
- 1,516
- Gender
- Male
- HSC
- 2024
Does anyone have a cheat sheet for proving shapes in complex numbers? Whenever I'm given a question like "prove these complex points form a parallelogram" I never know how to prove it and the answer's always smthn random like "the diagonals bisect each other". So is there a method of knowing the proof for each shape?
Average Boreduser
Rising Renewal
just look up properties lol. no way of getting around thatDoes anyone have a cheat sheet for proving shapes in complex numbers? Whenever I'm given a question like "prove these complex points form a parallelogram" I never know how to prove it and the answer's always smthn random like "the diagonals bisect each other". So is there a method of knowing the proof for each shape?
liamkk112
Well-Known Member
- Joined
- Mar 26, 2022
- Messages
- 1,101
- Gender
- Female
- HSC
- 2023
u just got to memorise the quadrilateral properties no way around itDoes anyone have a cheat sheet for proving shapes in complex numbers? Whenever I'm given a question like "prove these complex points form a parallelogram" I never know how to prove it and the answer's always smthn random like "the diagonals bisect each other". So is there a method of knowing the proof for each shape?
usually though:
- parallelogram -> pairs of equal side lengths, parallel sides
- square -> equal side lengths, 90 degrees between sides, parallel sides
- rectangle -> 90 degrees between sides, parallel sides
- rhombus -> pairs of equal side lengths, parallel sides, diagonals meet at 90 degrees and bisect
there r also kites but i forget how those work and they're relatively uncommon
There is always a purely algebraic method, which is usually awful. There are sometimes purely geometric methods (like for arg(z - i) = arg(z + 1) etc.). If there isn't an obvious purely geometric approach, the efficient answer is likely to involve:Does anyone have a cheat sheet for proving shapes in complex numbers? Whenever I'm given a question like "prove these complex points form a parallelogram" I never know how to prove it and the answer's always smthn random like "the diagonals bisect each other". So is there a method of knowing the proof for each shape?
- treating the complex numbers as vectors
- looking for geometric properties that proves the required result
- demonstrating these properties through algebraic representation of vectors
A diagram should make it obvious that side OB is adjacent to side OA in the square.
Properties of a square then dictate that OB = i.OA, and so the complex number iz represents B.
Then, using vector reasoning:
Hence, the point C is represented by z(1 + i), and so is in the second quadrant if
from the diagram (as A must be in quadrant 1 and, for C to be in quadrant 2 given angle COA is 45 degrees, OA must be inclined at at least 45 degrees above the real axis), or (algebraically), by solving:





