-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Need help with Surds men (1 Viewer)
- Thread starter youngsky
- Start date
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
1.
(Slow and steady, since I believe you are only beginning this topic)
(For simplicity simplify the second term)
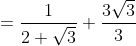
Rationalise the first expression by multiplying it with its conjugate, ie. 2-sqrt(3). We do this so we have a difference between two squares - eliminating the surd expression on the denominator.
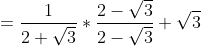
^2}+\sqrt{3})
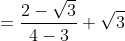
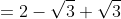
The number two belongs to the set of rational numbers. (A number that can be expressed in the quotient form p/q where q is not 0.)
2.
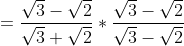
Rationalise it by multiplying by the conjugate of the denominator
^2}{\sqrt{3}^2-\sqrt{2}^2})
By the equality of surds,
3. See if you can use a similiar technique to do the last question. Start by expanding the left hand side.
(Slow and steady, since I believe you are only beginning this topic)
(For simplicity simplify the second term)
Rationalise the first expression by multiplying it with its conjugate, ie. 2-sqrt(3). We do this so we have a difference between two squares - eliminating the surd expression on the denominator.
The number two belongs to the set of rational numbers. (A number that can be expressed in the quotient form p/q where q is not 0.)
2.
Rationalise it by multiplying by the conjugate of the denominator
By the equality of surds,
3. See if you can use a similiar technique to do the last question. Start by expanding the left hand side.
Last edited:
Thanks for the help!
@Spiral: For question 8 (the second one) when I multiplied by the conjugate I got the answer x = 5, y = 2. I think you forgot to include the other negative root 6
@asianese: Can you explain the equating the rational/irrational parts method? Don't think I've done this before.
@Spiral: For question 8 (the second one) when I multiplied by the conjugate I got the answer x = 5, y = 2. I think you forgot to include the other negative root 6
@asianese: Can you explain the equating the rational/irrational parts method? Don't think I've done this before.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Very well spotted. A mistake on my part. Thank you for correcting me.
^2)
Is indeed
Is indeed
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
From Asianese's line:
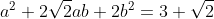
Notice on the RHS, we have something in the form
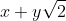
We can arrange the LHS into the form,
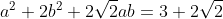
And by the equality of surds. (Just like equating coefficients for polynomials) We have our two equations of -
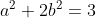
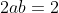
Notice on the RHS, we have something in the form
We can arrange the LHS into the form,
And by the equality of surds. (Just like equating coefficients for polynomials) We have our two equations of -
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Thank you for pointing it out Sir. Well spotted.