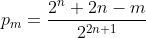Anyway here's my working out/thought process. Some one might be able to see what's going on.
To find
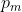
we will find the amount of ways we can have a string of 'n' heads after exactly 'm' throws, then divide by the total amount of possibilities.
Now the total amount of possibilities is just
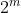
as there are 'm' throws, two outcomes.
Now for the other bit. The last n+1 throws must be T, H, H, ..., H, H to have a run of 'n' heads after 'm' throws. So this can only happen in one way, and thus we only need to find the amount of ways to arrange the first m-n-1 throws without having a string of 'n' heads.
To do this, we will find the amount of possibilities where we do have a string of 'n' heads, and subtract this from the total ways of arranging the first m-n-1 throws.
So assume we have a run of 'n' heads, and call this element A. Now we have to arrange the element A amongst m-2n-1 throws. Element A can be placed in (m-2n) positions, and the rest of the throws have two possibilities each - T or H. So we end up with the total ways being:
2^{m-2n-1})
The logic behind this is that it also contains the cases where we have a string of 'n+k' heads as we have a minimum of 'n' heads, and by "randomising" the remaining throws, it is possible for us to end up with a larger string of heads.
So the total ways where we don't get a string of 'n' heads is:
2^{m-2n-1})
Dividing this by the total ways gives:
2^{m-2n-1}}{2^m})
After some simplifying: