A vertical wall, height h metres, stands on a horizontal ground. When a projectile is fired, in a vertical plane which is right angles to the wall, from a point on the ground c metres from the wall, it just clears the wall at the highest point of its path.
The equations of motion for the projectile with angle of projectile [maths]\theta[/maths] are:
[maths]x=Vtcos\theta \ y=Vtsin\theta-\frac{1}{2}gt^2[/maths]
(i) show that the particle reaches the highest point on its parth when [maths]t=\frac{Vsin\theta}{g}[/maths]
(ii) Show that the speed of projection is given by [maths]V^2 = \frac{g}{2h}(4h^2+c^2)[/maths]
(iii) Find the angle of projection,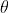 in terms of h and c.
in terms of h and c.
Thanks
The equations of motion for the projectile with angle of projectile [maths]\theta[/maths] are:
[maths]x=Vtcos\theta \ y=Vtsin\theta-\frac{1}{2}gt^2[/maths]
(i) show that the particle reaches the highest point on its parth when [maths]t=\frac{Vsin\theta}{g}[/maths]
(ii) Show that the speed of projection is given by [maths]V^2 = \frac{g}{2h}(4h^2+c^2)[/maths]
(iii) Find the angle of projection,
Thanks
