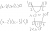When representing a quadratic inequality, say (x-2)(x-5) > 0 on the Cartesian plane, do you shade the areas above y=0 and outside the parabola, or do you simply emboss the part of actual parabola itself that's above y=0 with open circles at the x-intercepts? Or does either way not matter?
Similarly for (x-2)(x-5) < 0, do you shade inside of the parabola under y=0, or do you emboss the part parabola itself that's below y=0 and draw open circles at the x-intercepts? Or does it not matter which way I choose?
Similarly for (x-2)(x-5) < 0, do you shade inside of the parabola under y=0, or do you emboss the part parabola itself that's below y=0 and draw open circles at the x-intercepts? Or does it not matter which way I choose?