What does that mean? I see it a lot, but I fail to see the algebra manipulation. I learnt to read/comprehend "ln a = b" as "e to power b equals a" - there is no use of math ("raise both sides by e") here but simply definition.
I don't know if that is the official jargon for doing:
 to raise both sides by 10 is
to raise both sides by 10 is
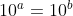
But I use those words to explain it
right, ok. That kind of makes sense, I guess it's just one of those processes I have to remember. Thank you. There will be more!
I haven't had proper teaching on this subject unfortunately so it's shaky as hell and I have very limited time to learn it before an exam.
When I want to eliminate "ln" from one side, I have to make the other side a power of "e".
Just think about what a logarithm means, a logarithm is the opposite of exponentiation, so to get rid of a logarithm, we simply exponentiate, this is the same logic when doing:
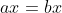
What do we want to get rid of? We want to get rid of a
multiplication of x, and to 'undo' this process, we simply 'divide' by x.
The point I'm trying to make here is, don't simply take it as a rote learnt concept, understand why you are doing what you are doing.
