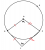
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ \textrm{Construct a circle passing through the points A, B and D, and let the center of the circle be O.}\\ \angle AOB=2\angle ADB~\textrm{(Angle at centre is twice the angle at the arc)}\\ ~\\ \textrm{But,}~ \angle ACB=2\angle ADB\\ \therefore \angle ACB=\angle AOB\\ ~\\ \textrm{Now,}~AC=BC~\textrm{(given) and}~AO=BO~\textrm{(radius of circle ABD)}\\ ~\\ \textrm{Hence, O and C are the same point - i.e. C is the centre of circle ABD}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ \textrm{Construct a circle passing through the points A, B and D, and let the center of the circle be O.}\\ \angle AOB=2\angle ADB~\textrm{(Angle at centre is twice the angle at the arc)}\\ ~\\ \textrm{But,}~ \angle ACB=2\angle ADB\\ \therefore \angle ACB=\angle AOB\\ ~\\ \textrm{Now,}~AC=BC~\textrm{(given) and}~AO=BO~\textrm{(radius of circle ABD)}\\ ~\\ \textrm{Hence, O and C are the same point - i.e. C is the centre of circle ABD}" title="\\ \textrm{Construct a circle passing through the points A, B and D, and let the center of the circle be O.}\\ \angle AOB=2\angle ADB~\textrm{(Angle at centre is twice the angle at the arc)}\\ ~\\ \textrm{But,}~ \angle ACB=2\angle ADB\\ \therefore \angle ACB=\angle AOB\\ ~\\ \textrm{Now,}~AC=BC~\textrm{(given) and}~AO=BO~\textrm{(radius of circle ABD)}\\ ~\\ \textrm{Hence, O and C are the same point - i.e. C is the centre of circle ABD}" /></a>
Not entirely happy with the way I've worded this, but it's late and I'm tired.