-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012 MX1 Marathon #1 (archive) (1 Viewer)
- Thread starter nightweaver066
- Start date
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
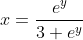
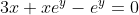
=-3x)
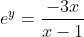
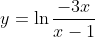
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 195
- Gender
- Male
- HSC
- 2011
Re: 2012 HSC MX1 Marathon
x = (e^y)/(3+e^y) = 1 - 3/(3+e^y)
so 3/(3 + e^y) = 1 - x
so 3/(1-x) = 3+e^y
so y = ln[3/(1-x) - 3]
You do polynomial division.how would i find the inverse of y = e^x/(3 + e^x)
i get stuck on x(3+e^y) = e^y
x = (e^y)/(3+e^y) = 1 - 3/(3+e^y)
so 3/(3 + e^y) = 1 - x
so 3/(1-x) = 3+e^y
so y = ln[3/(1-x) - 3]
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
EDIT: Oh it is unrelated to the differentiation question haha.
I do not understand why you would need to find the inverse of the function.how would i find the inverse of y = e^x/(3 + e^x)
i get stuck on x(3+e^y) = e^y
EDIT: Oh it is unrelated to the differentiation question haha.
Timske
Sequential
- Joined
- Nov 23, 2011
- Messages
- 794
- Gender
- Male
- HSC
- 2012
- Uni Grad
- 2016
Re: 2012 HSC MX1 Marathon
dont know just trying to do what this sheet is askingI do not understand why you would need to find the inverse of the function.
EDIT: Oh it is unrelated to the differentiation question haha.
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
<a href="http://www.codecogs.com/eqnedit.php?latex=\textsl{Prove that the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}@plus;... \textsl{ diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" title="\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" /></a>
<a href="http://www.codecogs.com/eqnedit.php?latex=\textsl{Prove that the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}@plus;... \textsl{ diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" title="\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" /></a>
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
A good Extension 2 student may be able to relate it to upper rectangles for the curve y=1/x and show that since the area is unbounded as x --> infinity, so is the series.
However, I don't think this will happen for an Extension 1 student.
Umm, I don't think the average MX1 student will be able to *rigorously* prove the divergence of the Harmonic Series.<a href="http://www.codecogs.com/eqnedit.php?latex=\textsl{Prove that the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}@plus;... \textsl{ diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" title="\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" /></a>
A good Extension 2 student may be able to relate it to upper rectangles for the curve y=1/x and show that since the area is unbounded as x --> infinity, so is the series.
However, I don't think this will happen for an Extension 1 student.
Re: 2012 HSC MX1 Marathon
This question is best suited to harder 3u, which is apart of the 4u course, not 3u, and yes as carrot said<a href="http://www.codecogs.com/eqnedit.php?latex=\textsl{Prove that the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}@plus;... \textsl{ diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" title="\textsl{Prove that the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \textsl{ diverges}" /></a>
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
<a href="http://www.codecogs.com/eqnedit.php?latex=\textup{It is known that the series }1@plus;\frac{1}{2}@plus;\frac{1}{4}@plus;\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}... \textup{diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textup{It is known that the series }1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{diverges}" title="\textup{It is known that the series }1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{diverges}" /></a>
With a bit of thinking, a good 3U student (I think) should be able to get it but this proof might not be fully rigourous...
What about now:This question is best suited to harder 3u, which is apart of the 4u course, not 3u, and yes as carrot said
<a href="http://www.codecogs.com/eqnedit.php?latex=\textup{It is known that the series }1@plus;\frac{1}{2}@plus;\frac{1}{4}@plus;\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}... \textup{diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textup{It is known that the series }1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{diverges}" title="\textup{It is known that the series }1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{diverges}" /></a>
With a bit of thinking, a good 3U student (I think) should be able to get it but this proof might not be fully rigourous...
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
If there is some series A_n that diverges and there exists another series B_n such that B_n > A_n, then B_n also diverges.
The proof is valid.What about now:
<a href="http://www.codecogs.com/eqnedit.php?latex=\textup{It is known that the series }1@plus;\frac{1}{2}@plus;\frac{1}{4}@plus;\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1@plus;\frac{1}{2}@plus;\frac{1}{3}@plus;\frac{1}{4}... \textup{diverges}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textup{It is known that the series }1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{diverges}" title="\textup{It is known that the series }1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}... \textup{ converges to 2}. \\ \textup{By comparing the series } 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{ to a geometric sequence where the ratio is not less than one, prove} \\\textup{that }1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}... \textup{diverges}" /></a>
With a bit of thinking, a good 3U student (I think) should be able to get it but this proof might not be fully rigourous...
If there is some series A_n that diverges and there exists another series B_n such that B_n > A_n, then B_n also diverges.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Consider the equation y=x^n + nx + 1.
Find the condition such that the curve has a stationary point with integer co-ordinates.
Find the co-ordinates of the stationary point in terms of n.
Consider the equation y=x^n + nx + 1.
Find the condition such that the curve has a stationary point with integer co-ordinates.
Find the co-ordinates of the stationary point in terms of n.
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 195
- Gender
- Male
- HSC
- 2011
Re: 2012 HSC MX1 Marathon
Also, sorry man for not talking to you today outside the timetabling unit
Is that sorta stuff like, allowed/used in 3u, when people dont really even know what converges/diverges mean?The proof is valid.
If there is some series A_n that diverges and there exists another series B_n such that B_n > A_n, then B_n also diverges.
Also, sorry man for not talking to you today outside the timetabling unit
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
I was actually going through the Analysis course notes whilst waiting for another BOS'er you are familiar with.
Haha nws =)Is that sorta stuff like, allowed/used in 3u, when people dont really even know what converges/diverges mean?
Also, sorry man for not talking to you today outside the timetabling unit
I was actually going through the Analysis course notes whilst waiting for another BOS'er you are familiar with.
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
<a href="http://www.codecogs.com/eqnedit.php?latex=y=x^n@plus;nx@plus;1\\ y'=nx^{n-1}@plus;n=n(x^{n-1}@plus;1)\\ $Stationary points occur when $y'=0\\ n(x^{n-1}@plus;1)=0\\ \therefore x^{n-1}=-1\\ $Hence, for there to be a stationary point with integer coordinates $n$ must be even since $n-1$ must be odd$\\ \therfore x=-1\\ y=(-1)^n@plus;n(-1)@plus;1\\ ~~~=1-n@plus;1$ (Since n is even)$\\ ~~~=2-n\\ \therefore $ the coordinates of the stationary point are $(-1,2-n)" target="_blank"><img src="http://latex.codecogs.com/gif.latex?y=x^n+nx+1\\ y'=nx^{n-1}+n=n(x^{n-1}+1)\\ $Stationary points occur when $y'=0\\ n(x^{n-1}+1)=0\\ \therefore x^{n-1}=-1\\ $Hence, for there to be a stationary point with integer coordinates $n$ must be even since $n-1$ must be odd$\\ \therfore x=-1\\ y=(-1)^n+n(-1)+1\\ ~~~=1-n+1$ (Since n is even)$\\ ~~~=2-n\\ \therefore $ the coordinates of the stationary point are $(-1,2-n)" title="y=x^n+nx+1\\ y'=nx^{n-1}+n=n(x^{n-1}+1)\\ $Stationary points occur when $y'=0\\ n(x^{n-1}+1)=0\\ \therefore x^{n-1}=-1\\ $Hence, for there to be a stationary point with integer coordinates $n$ must be even since $n-1$ must be odd$\\ \therfore x=-1\\ y=(-1)^n+n(-1)+1\\ ~~~=1-n+1$ (Since n is even)$\\ ~~~=2-n\\ \therefore $ the coordinates of the stationary point are $(-1,2-n)" /></a>Consider the equation y=x^n + nx + 1.
Find the condition such that the curve has a stationary point with integer co-ordinates.
Find the co-ordinates of the stationary point in terms of n.
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon

Also adding on to part iii), find the percentage error of the approximate and actual area.

Also adding on to part iii), find the percentage error of the approximate and actual area.
kingkong123
Member
- Joined
- Dec 20, 2011
- Messages
- 98
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
<a href="http://www.codecogs.com/eqnedit.php?latex=\textup{A function is }y=f(x)\textup{ is given in parimetric form by }x=tan\theta \textup{ and }\\y=4sin2\theta\textup{ for }\frac{-\pi}{2}<\theta<\frac{\pi}{2}.\textup{ State the domain and range of the function and show that }\\y=\frac{8x}{1@plus;x^{2}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textup{A function is }y=f(x)\textup{ is given in parimetric form by }x=tan\theta \textup{ and }\\y=4sin2\theta\textup{ for }\frac{-\pi}{2}<\theta<\frac{\pi}{2}.\textup{ State the domain and range of the function and show that }\\y=\frac{8x}{1+x^{2}}" title="\textup{A function is }y=f(x)\textup{ is given in parimetric form by }x=tan\theta \textup{ and }\\y=4sin2\theta\textup{ for }\frac{-\pi}{2}<\theta<\frac{\pi}{2}.\textup{ State the domain and range of the function and show that }\\y=\frac{8x}{1+x^{2}}" /></a>
<a href="http://www.codecogs.com/eqnedit.php?latex=\textup{A function is }y=f(x)\textup{ is given in parimetric form by }x=tan\theta \textup{ and }\\y=4sin2\theta\textup{ for }\frac{-\pi}{2}<\theta<\frac{\pi}{2}.\textup{ State the domain and range of the function and show that }\\y=\frac{8x}{1@plus;x^{2}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textup{A function is }y=f(x)\textup{ is given in parimetric form by }x=tan\theta \textup{ and }\\y=4sin2\theta\textup{ for }\frac{-\pi}{2}<\theta<\frac{\pi}{2}.\textup{ State the domain and range of the function and show that }\\y=\frac{8x}{1+x^{2}}" title="\textup{A function is }y=f(x)\textup{ is given in parimetric form by }x=tan\theta \textup{ and }\\y=4sin2\theta\textup{ for }\frac{-\pi}{2}<\theta<\frac{\pi}{2}.\textup{ State the domain and range of the function and show that }\\y=\frac{8x}{1+x^{2}}" /></a>
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Adding to that, show that the percentage error --> 0 as n approaches infinity.
Also adding on to part iii), find the percentage error of the approximate and actual area.
zeebobDD
Member
- Joined
- Oct 23, 2011
- Messages
- 411
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon

coulda done it for my test coming up next week if it wasnt cos inverse
Also adding on to part iii), find the percentage error of the approximate and actual area.
Timske
Sequential
- Joined
- Nov 23, 2011
- Messages
- 794
- Gender
- Male
- HSC
- 2012
- Uni Grad
- 2016
Re: 2012 HSC MX1 Marathon
zomg yallah habib cant do this
int0~1 2x/(2x + 1)^2 using u = 2x + 1 , x = (u-1)/2
x: 0 ~ 1
u: 3~4
du/dx = 2
dx = du/2
int3~4 2((u-1)/2))/u^2 * du/2
int3~4 ((u-1)/2)/u^2 * du
int3~4 (u-1)/2u^2 * du
i get stuck here..
zomg yallah habib cant do this
int0~1 2x/(2x + 1)^2 using u = 2x + 1 , x = (u-1)/2
x: 0 ~ 1
u: 3~4
du/dx = 2
dx = du/2
int3~4 2((u-1)/2))/u^2 * du/2
int3~4 ((u-1)/2)/u^2 * du
int3~4 (u-1)/2u^2 * du
i get stuck here..
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Split the fraction so you get two integrals.
Split the fraction so you get two integrals.
