What's the fastest way to simplify
^4+\left ( 1+\cos{\frac{\pi}{8}}-i\sin{\frac{\pi}{8}}\right )^4)
without expanding everything/using exact ratios?
Thanks!
without expanding everything/using exact ratios?
Thanks!
Haha fuark,Use double anges to eliminate the 1's. For example, cos(pi/8) becomes 2cos(pi/16)^2 -1 which will 'delete' the 1. Then use double angles on the sin(pi/8)=2sin(pi/16)cos(pi/16). Factorise and then De Moivre's- BOOOOOM.
Nice question though
Yeah I didn't know how to do that until there was a question in Terry Lee and that's where I learnt that wherever you have 1's in a trig equation, you can just 'delete' them like that. Its a nice trickHaha fuark,
Strong ability/10.
Did not notice that.
Does Terry have any other nice tricks in his book?Yeah I didn't know how to do that until there was a question in Terry Lee and that's where I learnt that wherever you have 1's in a trig equation, you can just 'delete' them like that. Its a nice trick
would you like to elaborate please?Or by geometry
You'll get it from school when we sign out.Does Terry have any other nice tricks in his book?
Perhaps I should buy it...
Ah ok, that's good. Hurry the eff up and sign outYou'll get it from school when we sign out.
Thanks! Just realised how it can also eliminate -1 with double angles as well. Will be sure to remember that next time hahaJust an addition: I was taught that, WHENEVER you see (1 + cos[something]) it should set off huge alarm bells. It's VERY likely that you need to use double angles to proceed =). Also, really helps to revise sum to products, and products to sum on the side (for those trickier 4u questions).
ThanksThis method is long, but what I have done is used the identity repeatedly of
This may not help with this question but it will certainly help you in the future. Good to find alternate ways than to use the traditional textbook methods.
The expression becomes,
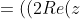)^2-2|z|^2)^2-2|z|^4)
