Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: MX2 Integration Marathon
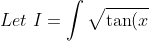}dx)
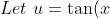, du=(1+\tan^{2}(x))dx)
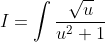
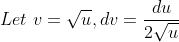
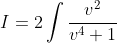
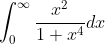
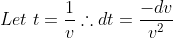
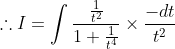
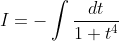
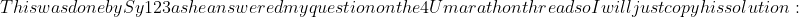
 )

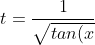}} )
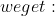
+log(\frac{1}{\sqrt{tanx}}^2+\sqrt{2} \frac{1}{\sqrt{tanx}}+1)-2 tan^{-1}(1- \sqrt{2}\frac{1}{\sqrt{tanx}})+2 tan^{-1}(\sqrt{2} \frac{1}{\sqrt{tanx}}+1) \right ))
Method 2: which I think is outside the syllabus:
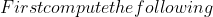
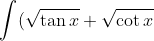 dx=\int\frac{\sin x +\cos x}{\sqrt{\sin x\cdot \cos x}}dx)
}{\sqrt{1-(\sin x -\cos x)^2}})

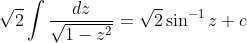
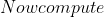
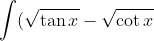dx)
}{\sqrt{(\sin x+\cos x)^2 -1} } dx)
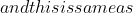
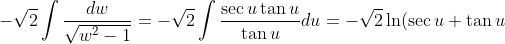+C)


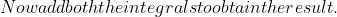
Method 1:
Method 2: which I think is outside the syllabus:
Last edited:

