Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 + \left( \binom{m+1}{m-2} + \binom{m+1}{m-3} \right) + \dots + \left(\binom{2m-2}{0} + \binom{2m-2}{1} \right ) + \binom{2m-1}{0} )
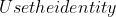
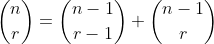

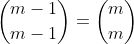
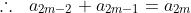
Do the same for n = 2k+1, and we then prove that:
 for all n, therefore it is the sequence of Fibonacci numbers.
for all n, therefore it is the sequence of Fibonacci numbers.
-----

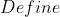
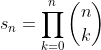
}{\left(\frac{s_{n}}{s_{n-1}} \right)} = e )
Do the same for n = 2k+1, and we then prove that:
-----

