Only heard of, never taught. Very well, will assume
Yes, best to do this for now.
A sketch of a possible proof though (about the lowest-tech one I can think of off the top of my head, although also the least general):
Given a sequence of real numbers, we define the limit superior of the sequence as
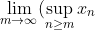)
. (You definitely will need to know what the supremum "sup" of a set of real numbers is, the existence of supremums for bounded sets is pretty much the defining property of the reals.)
You can prove the limit superior of any bounded sequence of reals exists by the monotone convergence theorem.
A corollary of this is that any bounded sequence of reals has a convergent subsequence.
Now suppose the c in your question did not exist. Then you could find a sequence x_n with f(x_n)->0.
Pass to a convergent subsequence y_n, and we must still have f(y_n)->0.
If y is the limit of y_n, then f(y)=0 by continuity. This contradicts the positivity of f and completes the proof.

