Professor X
New Member
- Joined
- Aug 8, 2009
- Messages
- 1
- Gender
- Male
- HSC
- N/A
Re: Australian Mathematics Competition








\,\,$)
)
\,\,$. Hence for every value of x there is 2 such values of y that give a palendrome that is divisible by 7$)

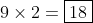
for the divisible by 7 one, I basically listed all the two digit numbers from 11 - 99 inclusive, and then reversed them.
e.g.
1111
1221
1331
1441
1551
etc
I know that the answer is definitely more than 15.

