Australian Maths Competition (2 Viewers)

[Professor X]

Re: Australian Mathematics Competition

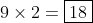
for the divisible by 7 one, I basically listed all the two digit numbers from 11 - 99 inclusive, and then reversed them.

e.g.
1111
1221
1331
1441
1551
etc

I know that the answer is definitely more than 15.

 

[Kajixtatsu]

Re: Australian Mathematics Competition

Alternative prrof for the palindromic numbers question,

Let number be abba = (1000)a + (1)a + (100)b + (10)b
= (1001)a + (110)b
= 11(13x7)a + 11(10b)
= 11(13x7a + 10b)

therefore abba = 11(13x7a + 10b)

and to have a number divisible by 7 10b must be divisible by 7, therefore b = 7
so your only numbers are 1001, 2002, 3003... 9009 & 1771, 2772... 9779.

 

[Timothy.Siu]

Re: Australian Mathematics Competition

I actually get 84 for this one *

my solution:

Spoiler

if you unfold the 3D shape into its net (only the side facing you, and with the dots) then you get a sort of double rhombus. the shortest distance is then found simply by connecting the two points with a line, and finding its length with pythagoras

i put 84 too.but that was a guess.

 

[Aquawhite]

Re: Australian Mathematics Competition

Did anyone spend enough time on the final question to complete it and come up with an answer?

This is the Senior Paper.

 

[lolokay]

Re: Australian Mathematics Competition

Iruka posted their solution to Q30 on the previous page
http://community.boredofstudies.org...n-mathematics-competition/17.html#post4503758

 

[Official]

Re: Australian Mathematics Competition

for the overlapping circles one, i drew, separately, two circles overlapping at opposite corners, and two circles overlapping at adjacent corner. from these, i found the values of different areas of the shapes in the four overlapping circles, and could then deduce the area of the section overlapped by all 4

Ah, so what did you get?

 

[lolokay]

Re: Australian Mathematics Competition

Ah, so what did you get?

c), which was 1-rt3+pi/3 iirc

 

[shaon0]

Re: Australian Mathematics Competition

c), which was 1-rt3+pi/3 iirc

Crap, I got pi-2sqrt(2). lol

 

[lolokay]

Re: Australian Mathematics Competition

does anyone know/has anyone posted the answer for Q29?

all I can think of is having a symmetrical arrangement of the stations, like if you placed a pentagon, square and inverted triangle on a circular railway track. this gives a value of 189

 

[Iruka]

Re: Australian Mathematics Competition

I am not sure if this is the correct answer (which is why I didn't post it earlier), and it sounds very counter intuitive, but if you let one of the Band C stations coincide and then put that point in the mid-point of the interval between two of the A stations then you can reduce the maximum distance between stations to 180.

 

[kiniki]

Re: Australian Mathematics Competition

for the ascending question, i got 246, using a bit of trial and error. did anyone else get similar? this test absolutely whipped me.

 

[Official]

Re: Australian Mathematics Competition

for the ascending question, i got 246, using a bit of trial and error. did anyone else get similar? this test absolutely whipped me.

Sorry, hate to burst your bubble but 246 * 6 = 1476, which is not an ascending number. The correct answer is infact 578.

 

[lolokay]

Re: Australian Mathematics Competition

I am not sure if this is the correct answer (which is why I didn't post it earlier), and it sounds very counter intuitive, but if you let one of the Band C stations coincide and then put that point in the mid-point of the interval between two of the A stations then you can reduce the maximum distance between stations to 180.

yeah, I would say that's it. I was sure i'd tested this set up too =/

 

[kiniki]

Re: Australian Mathematics Competition

Sorry, hate to burst your bubble but 246 * 6 = 1476, which is not an ascending number. The correct answer is infact 578.

what the helll how did i not pick that!?? i must of re done that question like 20 times coz i 'thought' it was the only one i knew haha
fail

 

[Official]

Re: Australian Mathematics Competition

Can someone confirm the answers to Qs 19 and 22?

 

[PC]

Re: Australian Mathematics Competition

19 = [5(3 – √3)]/2

22 = 12(5√3 + 9)

 

[Official]

Re: Australian Mathematics Competition

19 = [5(3 – √3)]/2

22 = 12(5√3 + 9)

Thanks

 

[maths94]

Re: Australian Mathematics Competition

I am not quite sure what number question it was, but it was a 10 mark question. It was in the intermediate division. The question was on patterns, it showed pattern 1,2 and 3 then it said what would pattern 11 be. My answer was 66, and i am very confident on that. So can anybody help me out.
....
<>
....

Pattern 1^
----
.....<>
<>
.....<>
......
Pattern 2^
...
........<>
...<>
<>...<>
...<>
.......<>
...
Pattern 3^
What is pattern 11? That was the question im pretty sure, thank you in advanced for replys. <>=hexagon

I will try and describe how i worked it out. Pattern 1 has one hexagon, while pattern 2 has three hexagon. So if i add 2 + 1=3 i got the one from the hexagon in pattern 1 and the two from the pattern (2)<--....Pattern 3 if we add three hexagons to pattern 2 thats gives us 6 and it also gives us pattern 3. So basically the next hexagon pattern 4 i would add 4 hexagons to the previous pattern. So its basically 6 hexagons from pattern 3 so i did.....6+4+5+6+7+8+9+10+11=66

 

[Iruka]

Re: Australian Mathematics Competition

yeah, I would say that's it. I was sure i'd tested this set up too =/

I have found a way to make the maximum distance 174 km. But i am still not happy with this result. Even though i do think that is the opitmal solution, I have done it in such an ad hoc manner that I can't be sure... I am sure that there is some far more elegant solution, if I could only think what it was... (sigh).

 

[gurmies]

Re: Australian Mathematics Competition

I have found a way to make the maximum distance 174 km. But i am still not happy with this result. Even though i do think that is the opitmal solution, I have done it in such an ad hoc manner that I can't be sure... I am sure that there is some far more elegant solution, if I could only think what it was... (sigh).

Take some solace from the fact that you solved the last question so brilliantly.