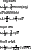Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Re: HSC 2012 Marathon 
That's it. Can't believe everyone struggled on that one so much! LOL<a href="http://www.codecogs.com/eqnedit.php?latex=tan(\theta ) = -4 @plus; 3\sqrt{3}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?tan(\theta ) = -4 + 3\sqrt{3}" title="tan(\theta ) = -4 + 3\sqrt{3}" /></a>
Barb please say yes