Re: 2012 HSC MX2 Marathon
It makes sense in my mind, but I'll try my best to explain what I was doing in words:
1. When we expand the product (1-a_k), we get the the expression 1 - sum a_i_1 + sum a_i_2 - sum a_i_3 + ... and this continues on until we have sum a_i_n, which is essentially the same thing as prod a_k.
2. Recognise that the first two terms are the RHS of the question, so it follows that if we prove sum a_i_2 - sum a_i_3 + ... +/- prod a_k is positive and nonzero, then the strict inequality is proved.
3. Now, we have to prove that the cyclic sums satisfy a_i_2 > sum a_i_3 > sum a_i_4 > ... > sum a_i_n (which is the same as product in this case).
4. We know trivially that
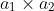
will be less than
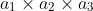
etc because a_k is between 0 and 1, so the more a_k we have, the smaller the value. Now we have to prove that the CYCLIC sum of such terms preserves the inequality.
5. So I set up an array
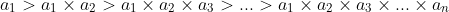
. But now, I want to set up a parallel array but with different terms in each inequality such that when added, the different combinations from these arrays will construct the cyclic sum.
6. Firstly, note that the a's range from a_1 to a_n. My first parallel array (the inequalities will still hold) will be
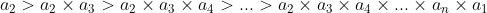
(Note that it 'cycles' back to the original a_1).
7. My second parallel array will be
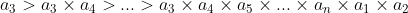
8. This process repeats n times so our last array will be
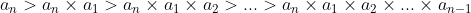
9. So if we add up all the arrays, we get something like what we need. But we have only considered consecutive groupings! What about product groupings like
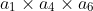
?? We will need those in order to properly construct the cyclic sum.
10. So as you can imagine we must now count the number of possible combinations in the cyclic sum and consider the MAX of them (let this be M) and this means we have to make M arrays in order to satisfy all term of the expansion. By doing so, it means we have all bases covered ranging from sum a_i_1 (which has the fewest combinations, namely C(n,1) all the way up to sum a_i_n (which will consequently have the same number of combinations as sum a_i_1 due to symmetry of Pascal's Triangle). So obviously, this will mean that we will have 'repeats' of the sums with fewer terms (like sum a_i_1), but this is okay because that means once we add them sum, we will just have some constant multiple of the bare minimum that we need for the sum of the arrays to construct a cyclic sum.
*Now I just realised where things can go wrong. This means we must prove that EVEN with this constant multiple, the inequality is preserved because the multiple could very easily imbalance the inequality and actually FLIP it around!*. I don't think the proof for this will be easy. It surely MUST be true (otherwise the identity doesn't work, and by induction we know it to be true) but the question now is HOW.
Sigh.

