Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (3 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
^{n-1} )
^n \geq \frac{1}{n+1} \ \ \ (*) )
This is what we need to prove, transforming the above AM-GM inequality:
^n \geq a_1 a_2 \dots a_n )
So we simply need to select numbers a_1, a_2, ... , a_n so that we get (*)
For simplicity sake, let
Now we find a_1 so that we yield (*)
 )

Yielding)^n > 1/(n+1) ) yielding the wanted inequality.
yielding the wanted inequality.
First transforming the wanted inequality so its easier to solve:
This is what we need to prove, transforming the above AM-GM inequality:
So we simply need to select numbers a_1, a_2, ... , a_n so that we get (*)
For simplicity sake, let
Now we find a_1 so that we yield (*)
Yielding
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
In the past people have asked for solutions to a lot of these questions, and I thought this thread would be of little benefit to people if they don't know the solutions to these questions.
Because some people want to know solutions of these questions?I like how you answer your own questions
In the past people have asked for solutions to a lot of these questions, and I thought this thread would be of little benefit to people if they don't know the solutions to these questions.
Last edited:
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Re: HSC 2013 4U Marathon
^.I like how you answer your own questions
Makematics
Well-Known Member
Re: HSC 2013 4U Marathon
I appreciate da solutions!!
I appreciate da solutions!!
Re: HSC 2013 4U Marathon
Post solutions that does not involve divergence/convergence? Thx.A good Sydney grammar question
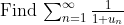
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon



 = \frac{1}{u_1} - \frac{1}{u_{N+1}} )
-> A Sydney Grammar teacher may be satisfied with simply the statement that u_n is increasing therefore 1/u_n converges to zero (I could be wrong, I don't know the marking criteria, however that is my guess), however a rigorous proof of the limit is given below:








I'm afraid you would have to prove the sum converges in order to find it, however I doubt that the Sydney grammar teachers who made this question expected students to do so.Post solutions that does not involve divergence/convergence? Thx.
-> A Sydney Grammar teacher may be satisfied with simply the statement that u_n is increasing therefore 1/u_n converges to zero (I could be wrong, I don't know the marking criteria, however that is my guess), however a rigorous proof of the limit is given below:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
A point P is chosen inside the unit square at random. What is the probability that P is closer to the centre of the square than any side thereof?
Bonus: Solve this for a cube, replacing the word "side" with "face".
A point P is chosen inside the unit square at random. What is the probability that P is closer to the centre of the square than any side thereof?
Bonus: Solve this for a cube, replacing the word "side" with "face".
Re: HSC 2013 4U Marathon
Thx Sy123.I'm afraid you would have to prove the sum converges in order to find it, however I doubt that the Sydney grammar teachers who made this question expected students to do so.
-> A Sydney Grammar teacher may be satisfied with simply the statement that u_n is increasing therefore 1/u_n converges to zero (I could be wrong, I don't know the marking criteria, however that is my guess), however a rigorous proof of the limit is given below:

RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
On first thoughts, you would just construct a circle within the square which has a radius a quarter that of the side length of the square. Then do the area of the circle divided by the area of the square. Similarly for the bonus, you construct a sphere and do the volume of the sphere divided by the volume of the cube.A point P is chosen inside the unit square at random. What is the probability that P is closer to the centre of the square than any side thereof?
Bonus: Solve this for a cube, replacing the word "side" with "face".
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Nah, the regions won't be circles and spheres.On first thoughts, you would just construct a circle within the square which has a radius a quarter that of the side length of the square. Then do the area of the circle divided by the area of the square. Similarly for the bonus, you construct a sphere and do the volume of the sphere divided by the volume of the cube.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Will check now...I didn't actually do the calculation.I got,
I want to figure out the bonus before I post my solution for this one.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 , (y-1/2)^2 > x-\frac{1}{4} ) ??
??
Its just 4 times the area bounded by the region (in the Cartesian plane where the square's co-ordinates are (0,0) (1,0) (1,1) and (0,1) ) ,Will check now...I didn't actually do the calculation.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
yeah that sounds about rightIts just 4 times the area bounded by the region (in the Cartesian plane where the square's co-ordinates are (0,0) (1,0) (1,1) and (0,1) ) ,??
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
And even then I still get the wrong answer because I don't know to find the area of a triangle properly and used the wrong base length.
I think it should be, and I'm not bothered to do the calculation again
^2 + \int_{1-1/\sqrt{2}}^{1/\sqrt{2}} \frac{1}{4} + (y- \frac{1}{2} )^2 \ dy \right) )
The above is supposed to be 4 times the area of the region bounded by the cartesian equations:


^2 < x-1/4 )
dem mistakes
Well firstly I found the complementary probability, the probability that its closer to the face instead :/I got:
(4*sqrt(2)-5)/3 and am pretty confident about it...
And even then I still get the wrong answer because I don't know to find the area of a triangle properly and used the wrong base length.
I think it should be, and I'm not bothered to do the calculation again
The above is supposed to be 4 times the area of the region bounded by the cartesian equations:
dem mistakes
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Yeah your equations are pretty similar to mine. Did mine quite carefully so am pretty sure its right. Will try the 3d one in a sec.Well firstly I found the complementary probability, the probability that its closer to the face instead :/
And even then I still get the wrong answer because I don't know to find the area of a triangle properly and used the wrong base length.
I think it should be, and I'm not bothered to do the calculation again
The above is supposed to be 4 times the area of the region bounded by the cartesian equations:
dem mistakes
- Status
- Not open for further replies.

