Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (3 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Re: HSC 2013 4U Marathon
Wassup guys, i'm part of the 2014 cohort, how do you guys post solutions in here? Latex only?
Anyways, a bit of an intro:
Like I said i'm in class of 2014 and basically gonna start coming on here more often cause this forum is awesome.
Subjects:
4 Unit Maths
Advanced English
Physics
Chemistry
ATAR GOAL: 97+ (But might as well reach for the stars right? 99? LOL)
Let me make my addition to this thread haha
Integrate secxtanx/sqrt(1-sec^2x) between b and a where b>a
BTW: Is it just 4u questions or can interesting 3u ones come in here as well?
Wassup guys, i'm part of the 2014 cohort, how do you guys post solutions in here? Latex only?
Anyways, a bit of an intro:
Like I said i'm in class of 2014 and basically gonna start coming on here more often cause this forum is awesome.
Subjects:
4 Unit Maths
Advanced English
Physics
Chemistry
ATAR GOAL: 97+ (But might as well reach for the stars right? 99? LOL)
Let me make my addition to this thread haha
Integrate secxtanx/sqrt(1-sec^2x) between b and a where b>a
BTW: Is it just 4u questions or can interesting 3u ones come in here as well?
Last edited:
Re: HSC 2013 4U Marathon
5-12i and 3+4i.
----------
z=4(1-i)+-sqrt(-63-16i) (After simplification) (Quadratic Formula)
----------
Delta=-63-16i
Root Delta= +-(1-8i)
-----------------------------
Therefore,
z=4-4i+-(1-8i)
z=5-12i and 3+4i
(Q2) Drew up parallelogram with z1 being on real axis and z2 being on imaginary axis. Then using head to tail etc etc.
Formed a square -> right angled triangles using diagonals.
In other words: (using pythagorus)
|z1|^2+|z2|^2=|z1+z2|^2 <-(1)
and
|z1|^2+|z2|^2=|z1-z2|^2 <-(2)
Now, (1)+(2):
|z1+z2|^2 + |z1-z2|^2 = 2(|z1|^2+|z2|^2)
Therefore, proven.
(Q3)-- Having problems knowing where to start, hint maybe? LOL
Anyways, thanks guys, this forum is awesome.
Keep the hard complex questions coming, 4u assessment is pure complex
(Q1)Put a new 2014 thread? I dislike years getting mixed up =[

5-12i and 3+4i.
----------
z=4(1-i)+-sqrt(-63-16i) (After simplification) (Quadratic Formula)
----------
Delta=-63-16i
Root Delta= +-(1-8i)
-----------------------------
Therefore,
z=4-4i+-(1-8i)
z=5-12i and 3+4i
(Q2) Drew up parallelogram with z1 being on real axis and z2 being on imaginary axis. Then using head to tail etc etc.
Formed a square -> right angled triangles using diagonals.
In other words: (using pythagorus)
|z1|^2+|z2|^2=|z1+z2|^2 <-(1)
and
|z1|^2+|z2|^2=|z1-z2|^2 <-(2)
Now, (1)+(2):
|z1+z2|^2 + |z1-z2|^2 = 2(|z1|^2+|z2|^2)
Therefore, proven.
(Q3)-- Having problems knowing where to start, hint maybe? LOL
Anyways, thanks guys, this forum is awesome.
Keep the hard complex questions coming, 4u assessment is pure complex
obliviousninja
(╯°□°)╯━︵ ┻━┻ - - - -
Re: HSC 2013 4U Marathon
there's a separate 3u thread, but if its under harder 3u, post here.Wassup guys, i'm part of the 2014 cohort, how do you guys post solutions in here? Latex only?
Anyways, a bit of an intro:
Like I said i'm in class of 2014 and basically gonna start coming on here more often cause this forum is awesome.
Subjects:
4 Unit Maths
Advanced English
Physics
Chemistry
ATAR GOAL: 97+ (But might as well reach for the stars right? 99? LOL)
Let me make my addition to this thread haha
Integrate secxtanx/sqrt(1-sec^2x) between b and a where b>a
BTW: Is it just 4u questions or can interesting 3u ones come in here as well?
Re: HSC 2013 4U Marathon
Alright. this might pass as harder 3u, not sure lol. It's pretty interesting for 4u anyways:
Just learning latex off others haha:
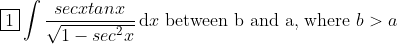
LOL My noob latex skillz.
Could someone tell me how to put boundaries on integration and seperate the dx from the fraction to make it look more nice
Thankyou
Alright. this might pass as harder 3u, not sure lol. It's pretty interesting for 4u anyways:
Just learning latex off others haha:
LOL My noob latex skillz.
Could someone tell me how to put boundaries on integration and seperate the dx from the fraction to make it look more nice
Thankyou
Last edited:
Kurosaki
True Fail Kid
Re: HSC 2013 4U Marathon

Is this what you mean?
Alright. this might pass as harder 3u, not sure lol. It's pretty interesting for 4u anyways:
Just learning latex off others haha:
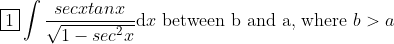
LOL My noob latex skillz.
Could someone tell me how to put boundaries on integration and seperate the dx from the fraction to make it look more nice
Thankyou
Is this what you mean?
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
Hints aren't welcomed here.Alright. this might pass as harder 3u, not sure lol. It's pretty interesting for 4u anyways:
Just learning latex off others haha:
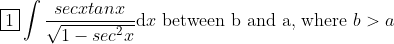
LOL My noob latex skillz.
Could someone tell me how to put boundaries on integration and seperate the dx from the fraction to make it look more nice
Thankyou
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: HSC 2013 4U Marathon
A string is attached to a mass and its other end attached to the pivot of a circular disk of radius R. The disk in on a shaft (assume the shaft and the disk is weightless) and the length of the string is h metres. The shaft rotates anticlockwise and as the speed of shaft increases the mass swings outward. Let the Mass be m and the disk rotates about its axle with a constant angular velocity. This constant angular velocity w produces an angle θ with the vertical.
a) Find the relation of w, h, R, g in terms of theta.
b) Use graphical means to show that for a given w there is just one value of theta in the range of 0<θ<pi/2 (less than or equal to symbol), which satisfies this relation.
c) Given R=6, h=2, θ=60 and g=10, find w relative to ground.
I cant seem to get part b). a nd c is done. Please help 2013 ers. Question open to all .
Thanks
A string is attached to a mass and its other end attached to the pivot of a circular disk of radius R. The disk in on a shaft (assume the shaft and the disk is weightless) and the length of the string is h metres. The shaft rotates anticlockwise and as the speed of shaft increases the mass swings outward. Let the Mass be m and the disk rotates about its axle with a constant angular velocity. This constant angular velocity w produces an angle θ with the vertical.
a) Find the relation of w, h, R, g in terms of theta.
b) Use graphical means to show that for a given w there is just one value of theta in the range of 0<θ<pi/2 (less than or equal to symbol), which satisfies this relation.
c) Given R=6, h=2, θ=60 and g=10, find w relative to ground.
I cant seem to get part b). a nd c is done. Please help 2013 ers. Question open to all .
Thanks
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Re: HSC 2013 4U Marathon
Alright. this might pass as harder 3u, not sure lol. It's pretty interesting for 4u anyways:
Just learning latex off others haha:
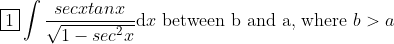
LOL My noob latex skillz.
Could someone tell me how to put boundaries on integration and seperate the dx from the fraction to make it look more nice
Thankyou
Alternatively you can use the \mathop{dx} command (mathematical operation) which spaces things nicely."\," is a common spacing string used to separate integrand from the "dx".
Re: HSC 2013 4U Marathon


Yeah, thanks
Is this what you mean?
Step back bro, too pro LOLHints aren't welcomed here.
Thanks, works great."\," is a common spacing string used to separate integrand from the "dx".
Shii, is this mechanics already?A string is attached to a mass and its other end attached to the pivot of a circular disk of radius R. The disk in on a shaft (assume the shaft and the disk is weightless) and the length of the string is h metres. The shaft rotates anticlockwise and as the speed of shaft increases the mass swings outward. Let the Mass be m and the disk rotates about its axle with a constant angular velocity. This constant angular velocity w produces an angle θ with the vertical.
a) Find the relation of w, h, R, g in terms of theta.
b) Use graphical means to show that for a given w there is just one value of theta in the range of 0<θ<pi/2 (less than or equal to symbol), which satisfies this relation.
c) Given R=6, h=2, θ=60 and g=10, find w relative to ground.
I cant seem to get part b). a nd c is done. Please help 2013 ers. Question open to all .
Thanks
Last edited:
bottleofyarn
Member
- Joined
- Sep 22, 2013
- Messages
- 50
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
I'm not sure if I'm missing a force or my diagram is wrong, but I get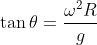 which is missing h. Graphing this for w>0, it has an inverse function (autonomous increase is the phrase I think) and so there is only one value for theta for any w.
which is missing h. Graphing this for w>0, it has an inverse function (autonomous increase is the phrase I think) and so there is only one value for theta for any w.
My answer for c) is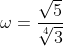 .
.
Also, is the pivot of the disc the centre?
Mechanics already!A string is attached to a mass and its other end attached to the pivot of a circular disk of radius R. The disk in on a shaft (assume the shaft and the disk is weightless) and the length of the string is h metres. The shaft rotates anticlockwise and as the speed of shaft increases the mass swings outward. Let the Mass be m and the disk rotates about its axle with a constant angular velocity. This constant angular velocity w produces an angle θ with the vertical.
a) Find the relation of w, h, R, g in terms of theta.
b) Use graphical means to show that for a given w there is just one value of theta in the range of 0<θ<pi/2 (less than or equal to symbol), which satisfies this relation.
c) Given R=6, h=2, θ=60 and g=10, find w relative to ground.
I cant seem to get part b). a nd c is done. Please help 2013 ers. Question open to all .
Thanks
I'm not sure if I'm missing a force or my diagram is wrong, but I get
My answer for c) is
Also, is the pivot of the disc the centre?
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
Monotone increasing would be a better phrase.Mechanics already!
I'm not sure if I'm missing a force or my diagram is wrong, but I getwhich is missing h. Graphing this for w>0, it has an inverse function (autonomous increase is the phrase I think) and so there is only one value for theta for any w.
My answer for c) is.
Also, is the pivot of the disc the centre?
bottleofyarn
Member
- Joined
- Sep 22, 2013
- Messages
- 50
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
That's the one.Monotone increasing would be a better phrase.
hayabusaboston
Well-Known Member
Re: HSC 2013 4U Marathon
Show that for n greater than 2, there are no positive integer solutions for a^n+b^n=c^n
Show that for n greater than 2, there are no positive integer solutions for a^n+b^n=c^n
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
So
a=b=3, c=4 solves the equation with n=log(1/2)/log(3/4).
Hence the claim is untrue.
"Positive integer solutions" means a,b,c must be positive integers. You have not restricted n though beyond saying that it is larger than 2.Show that for n greater than 2, there are no positive integer solutions for a^n+b^n=c^n
So
a=b=3, c=4 solves the equation with n=log(1/2)/log(3/4).
Hence the claim is untrue.
Re: HSC 2013 4U Marathon
Fermat's Last Theorem
No way, any of us on here could probably do it...
Anyways, Check it out,
http://en.wikipedia.org/wiki/Fermat's_Last_Theorem
and
https://www.youtube.com/watch?v=qiNcEguuFSA
UNLESS:
I'm not sure where you got this from but it is a very famous problem:Show that for n greater than 2, there are no positive integer solutions for a^n+b^n=c^n
Fermat's Last Theorem
No way, any of us on here could probably do it...
Anyways, Check it out,
http://en.wikipedia.org/wiki/Fermat's_Last_Theorem
and
https://www.youtube.com/watch?v=qiNcEguuFSA
UNLESS:
LOL nice one, caught on technicality? But pretty sure it's referring to fermat's last theorem. Where n must also be an integer."Positive integer solutions" means a,b,c must be positive integers. You have not restricted n though beyond saying that it is larger than 2.
So
a=b=3, c=4 solves the equation with n=log(1/2)/log(3/4).
Hence the claim is untrue.
Last edited:
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: HSC 2013 4U Marathon
Oh okkkkk... Right thanks. Yep mechanics is funn... I literally think mechanics is gonna be my best subject but havent done conics yet so cant say too much about the combination but mechanics with parametrics is yeh good, (physics seems like a kid in front of it- apparently i heard they took out mechanics from physsics and putit in four unit) nope the pivot is at the end of the circular disk thereby given radius R; If it was the centre of the disk and therfore the shaft , then i donot see why would it be required am i right? Thanks I got everything except the meaning of autonomous?Mechanics already!
I'm not sure if I'm missing a force or my diagram is wrong, but I getwhich is missing h. Graphing this for w>0, it has an inverse function (autonomous increase is the phrase I think) and so there is only one value for theta for any w.
My answer for c) is.
Also, is the pivot of the disc the centre?
Oh ok i get that.Monotone increasing would be a better phrase.
Whow How do you show that?> Is that harder ext 1?Show that for n greater than 2, there are no positive integer solutions for a^n+b^n=c^n
I dont get it."Positive integer solutions" means a,b,c must be positive integers. You have not restricted n though beyond saying that it is larger than 2.
So
a=b=3, c=4 solves the equation with n=log(1/2)/log(3/4).
Hence the claim is untrue.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
You'll be able to do it by half yearlies.
Don't worry about it. It was an unsolved problem for about 300 years until Wiles solves it in the 90's after progress and links from many previous mathematician's work.Whow How do you show that?> Is that harder ext 1?
You'll be able to do it by half yearlies.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: HSC 2013 4U Marathon
 . But hope so. What topic is it in?
. But hope so. What topic is it in?
haha i feel dumb,Don't worry about it. It was an unsolved problem for about 300 years until Wiles solves it in the 90's after progress and links from many previous mathematician's work.
You'll be able to do it by half yearlies.
- Status
- Not open for further replies.

