HSC 2013 MX2 Marathon (archive) (2 Viewers)

seanieg89 · Dec 9, 2013

Re: HSC 2014 4U Marathon

$Realise's inequality screams AM-GM. \\ \\ Indeed if we define $y_k:=\frac{1}{k}(a_k/a_{k+1})^{1/k}$, we can directly apply AM-GM to the sum $\sum_{k=1}^n\sum_{j=1}^k y_k$ containing $\frac{n(n+1)}{2}$ terms to obtain the result as well as the equality conditions.\\ \\ Alternatively, Lagrange Multipliers (my first method) gives a relatively quick and brainless way to solve such constrained optimisation problems.\\ \\ NB: I use the double summation notation just to emphasise that we are splitting the $ky_k$ into $k$ summands before our application of AM-GM.$

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

seanieg89 said:
$Realise's inequality screams AM-GM. \\ \\ Indeed if we define $y_k:=\frac{1}{k}(a_k/a_{k+1})^{1/k}$, we can directly apply AM-GM to the sum $\sum_{k=1}^n\sum_{j=1}^k y_k$ containing $\frac{n(n+1)}{2}$ terms to obtain the result as well as the equality conditions.\\ \\ Alternatively, Lagrange Multipliers (my first method) gives a relatively quick and brainless way to solve such constrained optimisation problems.\\ \\ NB: I use the double summation notation just to emphasise that we are splitting the $ky_k$ into $k$ summands before our application of AM-GM.$

Yep that was my method, I thought it was a really nice use of AM-GM. I came across a nice inequalities document too on google, might link.

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

Inequalities http://www.aam.org.in/site/st_material/14.pdf

seanieg89 · Dec 9, 2013

Re: HSC 2014 4U Marathon

RealiseNothing said:
Yep that was my method, I thought it was a really nice use of AM-GM. I came across a nice inequalities document too on google, might link.

I must admit, the AM-GM solution would be a bit harder to find if I didn't know Lagrange multipliers. (As the appropriate definition of y_k could potentially take a little time to spot.)

LM told me the equality conditions (each y_k as defined above must be equal.) From this fact as well as the fact that the problem reeked of AM-GM I figured an MX2 method would just be defining y_k as I did and using AM-GM.

If you don't already know LM you should learn about it, it's a very powerful and general method.

asianese · Dec 9, 2013

Re: HSC 2014 4U Marathon

RealiseNothing said:
Inequalities http://www.aam.org.in/site/st_material/14.pdf

Awkward moment when the first proof is:

$\dfrac{a+b}{2} \ge \sqrt{ab}$ which start off with

$Squaring, $ (a+b)^2 \ge 4ab $ which is equivalent to $ (a-b)^2 \ge 0 $ which is true. Thus the original statement is true.$

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

asianese said:
Awkward moment when the first proof is:

$\dfrac{a+b}{2} \ge \sqrt{ab}$ which start off with

$Squaring, $ (a+b)^2 \ge 4ab $ which is equivalent to $ (a-b)^2 \ge 0 $ which is true. Thus the original statement is true.$

That works for AM-GM though. $\sqrt{ab}\geq 0$

asianese · Dec 9, 2013

Re: HSC 2014 4U Marathon

I'm talking about assuming what was to be proved.

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

asianese said:
I'm talking about assuming what was to be proved.

You can do that for AM-GM?

seanieg89 · Dec 9, 2013

Re: HSC 2014 4U Marathon

asianese said:
I'm talking about assuming what was to be proved.

It's fine, all steps are obviously biconditional so it doesn't matter what end you start at. And you need this biconditionality to get the "iff" statement.

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

seanieg89 said:
It's fine, all steps are obviously biconditional so it doesn't matter what end you start at. And you need this biconditionality to get the "iff" statement.

This, which is why I put $\sqrt{ab} \geq 0$ as obviously the squaring will still preserve the direction of the inequality.

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

This isn't too hard, will have to do though until I think of something better.

Consider a polynomial with roots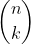 $\binom{n}{k}$ for $k=0, 1, 2, ..., n$

Find the sum of the roots two at a time.

Carrotsticks · Dec 9, 2013

Re: HSC 2014 4U Marathon

seanieg89 said:
It's fine, all steps are obviously biconditional so it doesn't matter what end you start at. And you need this biconditionality to get the "iff" statement.

To add on to this, think of it as building a two-laned road all one go rather than building one lane and then once you reach one end, go backwards to build the other lane.

This is often a good trick to kill of 'IFF' problems, but obviously you have to be very careful that everything you do is 'two laned', otherwise the other direction is immediately 'compromised'.

Sy123 · Dec 9, 2013

Re: HSC 2014 4U Marathon

I like this sum:

$$Find the sum for$ \ |x| < 1$

$\frac{x}{1+x} + \frac{2x^2}{1+x^2} + \frac{4x^4}{1+x^4} + \dots$

Carrotsticks · Dec 9, 2013

Re: HSC 2014 4U Marathon

I haven't tried the Q yet, but it looks pretty!

Sy123 · Dec 9, 2013

Re: HSC 2014 4U Marathon

RealiseNothing said:
This isn't too hard, will have to do though until I think of something better.

Consider a polynomial with roots $\binom{n}{k}$ for $k=0, 1, 2, ..., n$

Find the sum of the roots two at a time.

$\\ $Consider a set of$ \ n \ $distinct blue balls and$ \ n \ $distinct red balls. I will take any number of balls from the 2 boxes, that is, I can pick$ \ m \ $balls from the blue box and$ \ k \ $balls from the red box. The number of possibilities of such selections is$ \\ \\ \sum_{m,k \leq n} \binom{n}{m} \binom{n}{k}$

$\\$Alternatively we can consider the box together as$ \ 2n \ $balls, and therefore the number of possibilities of picking any number of balls from$ \ 2n \ $balls is$$

$\binom{2n}{0} + \binom{2n}{1} + \dots + \binom{2n}{2n} = 4^n$

$\\ $However we must consider counting terms such as$ \ \ \binom{n}{k}^2 \ \ $since they are not included in the initial sum, therefore we must take away$ \\ \\ \sum_{j=0}^n \binom{n}{j}^2 = \binom{2n}{n}$

$\\ $Hence we arrive at$ \\ \\ \sum_{m \neq k} \binom{n}{k} \binom{n}{m} = 4^n - \binom{2n}{n}$

$\\ $But we must make a distinction between$ \ \ \binom{n}{k} \binom{n}{m} \ \ $and$ \ \binom{n}{m} \binom{n}{k} \ \ $hence divide by 2 to get the final result$ \\ \\ \fbox{2^{2n-1} - \frac{1}{2} \binom{2n}{n}}$

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

Yep that's correct, but you double count I think, just divide by 2.

Sy123 · Dec 9, 2013

Re: HSC 2014 4U Marathon

RealiseNothing said:
Yep that's correct, but you double count I think, just divide by 2.

Ahh yes I see that, editing.

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

Sy123 said:
I like this sum:

$$Find the sum for$ \ |x| < 1$

$\frac{x}{1+x} + \frac{2x^2}{1+x^2} + \frac{4x^4}{1+x^4} + \dots$

So far I have this, not sure if it'll go anywhere. Will edit in my solution as I progress.

Consider the general k'th term:

$\frac{kx^k}{1+x^k} = \frac{kx^k+k-k}{1+x^k} = \frac{k(1+x^k) - k}{1+x^k} = k - \frac{k}{1+x^k}$

Now we just sum this:

$(1+2+4+8+...) - (\frac{1}{1+x} + \frac{2}{1+x^2} + ...)$

Alternative expression:

$\sum_{k=0}^{\infty} 2^k(1-\frac{1}{1+x^{2^k}})$

The second expression seems like it would be easier to evaluate atm.

nightweaver066 · Dec 9, 2013

Re: HSC 2014 4U Marathon

Sy123 said:
I like this sum:

$$Find the sum for$ \ |x| < 1$

$\frac{x}{1+x} + \frac{2x^2}{1+x^2} + \frac{4x^4}{1+x^4} + \dots$

$\frac{x}{1-x}?$

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

Sy123 said:
I like this sum:

$$Find the sum for$ \ |x| < 1$

$\frac{x}{1+x} + \frac{2x^2}{1+x^2} + \frac{4x^4}{1+x^4} + \dots$

Hmm I just tried a completely different method and got $\frac{x}{1-x}$

Is this right? I'll post my solution if it is.

HSC 2013 MX2 Marathon (archive) (2 Viewers)

Well-Known Member

what is that?It is Cowpea

what is that?It is Cowpea

Well-Known Member

Σ

what is that?It is Cowpea

Σ

what is that?It is Cowpea

Well-Known Member

what is that?It is Cowpea

what is that?It is Cowpea

Retired

This too shall pass

Retired

This too shall pass

what is that?It is Cowpea

This too shall pass

what is that?It is Cowpea

Well-Known Member

what is that?It is Cowpea

Users Who Are Viewing This Thread (Users: 0, Guests: 2)