HSC 2013 MX2 Marathon (archive) (2 Viewers)

RealiseNothing · Dec 9, 2013

Re: HSC 2014 4U Marathon

nightweaver066 said:
$\frac{x}{1-x}?$

Ok if you got it too I'm assuming it's right:

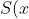$S(x) = \frac{x}{1+x} + \frac{2x^2}{1+x^2} + \frac{4x^4}{1+x^4} + ...$

$\frac{S(x)}{x} = \frac{1}{1+x} + \frac{2x}{1+x^2} + \frac{4x^3}{1+x ^4} + ...$

Now we have on the RHS, the numerator is the derivative of the denominator, so we shall integrate both sides:

$\int \frac{S(x)}{x} \dx = \ln(1+x) + \ln(1+x^2) + \ln(1+ x^4) + ...$

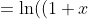$=\ln((1+x)(1+x^2)(1+x^4)...)$

$=\ln(1+x+x^2+x^3+x^4+...)$

$=\ln(\frac{1}{1-x})$

$=-\ln(1-x)$

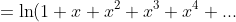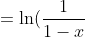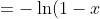So we have:

$\int \frac{S(x)}{x} = -\ln(1-x)$

Differentiating both sides:

$\frac{S(x)}{x} = \frac{1}{1-x}$

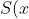$S(x) = \frac{x}{1-x}$

asianese · Dec 9, 2013

Re: HSC 2014 4U Marathon

That kind of question lends itself to a generating function type approach, as you have done Realise.

Sy123 · Dec 9, 2013

Re: HSC 2014 4U Marathon

Correct!

Though for a more rigorous solution I'd deal with the partial sum first but that's not much of an issue

Sy123 · Dec 10, 2013

Re: HSC 2014 4U Marathon

$\\ $The sum of the positive reals$ \ a_1, a_2 , \dots , a_n \ $is$ \ 1 \\ \\ $Show that$ \\ \\ \left(1 + \frac{1}{a_1}\right) \left(1 + \frac{1}{a_2} \right) \left(1 + \frac{1}{a_3} \right) \dots \left(1+ \frac{1}{a_n} \right) \geq (n+1)^n$

nightweaver066 · Dec 11, 2013

Re: HSC 2014 4U Marathon

Sy123 said:
$\\ $The sum of the positive reals$ \ a_1, a_2 , \dots , a_n \ $is$ \ 1 \\ \\ $Show that$ \\ \\ \left(1 + \frac{1}{a_1}\right) \left(1 + \frac{1}{a_2} \right) \left(1 + \frac{1}{a_3} \right) \dots \left(1+ \frac{1}{a_n} \right) \geq (n+1)^n$

Suppose w.l.o.g. that $1 > a_1 \geq a_2 \geq ... \geq a_n$ .

$(1+\frac{1}{a_1})(1+\frac{1}{a_2})...(1+\frac{1}{a_n})$

$\geq (1+\frac{1}{a_1})^n$

Now, consider the sum $a_1 + a_2 + ... + a_n \geq na_1$

As $a_1 + ... + a_n = 1$ , $1 \geq na_1$

$n \leq \frac{1}{a_1}$

$\therefore (1+\frac{1}{a_1})(1+\frac{1}{a_2})...(1+\frac{1}{a_n}) \geq (n+1)^n$

Sy123 · Dec 11, 2013

Re: HSC 2014 4U Marathon

nightweaver066 said:
Suppose w.l.o.g. that $1 > a_1 \geq a_2 \geq ... \geq a_n$ .

$(1+\frac{1}{a_1})(1+\frac{1}{a_2})...(1+\frac{1}{a_n})$

$\geq (1+\frac{1}{a_1})^n$

Now, consider the sum $a_1 + a_2 + ... + a_n \geq na_1$

As $a_1 + ... + a_n = 1$ , $1 \geq na_1$

$n \leq \frac{1}{a_1}$

$\therefore (1+\frac{1}{a_1})(1+\frac{1}{a_2})...(1+\frac{1}{a_n}) \geq (n+1)^n$

How would

$a_1 + a_2 + \dots +a_n \geq na_1$

Since $a_1$ is largest, the inequality sign should be reversed, meaning:

$\frac{1}{a_1} \leq n$

Which unfortunately cannot be allowed to 'be subbed in'

Sy123 · Dec 11, 2013

Re: HSC 2014 4U Marathon

$a,b,c > 1$

$\frac{1}{a^2 -1} + \frac{1}{b^2 -1} + \frac{1}{c^2-1} = 1$

$\\ $Prove that$ \\ \\ \frac{1}{a+1} + \frac{1}{b+1} + \frac{1}{c+1} \leq 1$

Fawun · Dec 11, 2013

Re: HSC 2014 4U Marathon

is this even complex numbers

asianese · Dec 11, 2013

Re: HSC 2014 4U Marathon

Fawun said:
is this even complex numbers

Such strong maff.

obliviousninja · Dec 11, 2013

Re: HSC 2014 4U Marathon

asianese said:
Such strong maff.

.

Fawun · Dec 11, 2013

Re: HSC 2014 4U Marathon

HSC 2014 = most of us have only learned complex numbers so...

Fawun · Dec 11, 2013

Re: HSC 2014 4U Marathon

we haven't even learned harder 3u inequalities so smh at this

Sy123 · Dec 11, 2013

Re: HSC 2014 4U Marathon

$\\ $i) Expand$ \ \ (1+i\sqrt{3})(1+i) \\ \\ $ii) Hence show that$ \ \ \cos \left(\frac{\pi}{24} \right) = \frac{1}{2} \sqrt{2 + \sqrt{2+\sqrt{3}}}$

If you want problems suited to a 2014er then I suggest posting some questions or answering the complex numbers that I have posted before

asianese · Dec 11, 2013

Re: HSC 2014 4U Marathon

Fawun here's an easy one:

$Prove, using mathematical induction, for $ n\ge1 $ that$

$(\cos\theta + i\sin\theta)^n = \cos(n\theta) + i\sin(n\theta).$

$$Generalise this formula for negative values of $n.$

$Does it make sense to extend the possible values of $ n$ to the complex numbers? That is, does it make sense to `raise' a complex number to another complex number? Provide examples to support your answer.$

Sy123 · Dec 11, 2013

Re: HSC 2014 4U Marathon

$\\ $i) By process of Mathematical Induction show that$ \\ \\ (\cos x + i\sin x)^n = \cos(nx) + i\sin(nx) \ \ $for integer$ \ n \\ \\ $ii) Find$ \ x \ $in terms of$ \ \theta \ $such that$ \\ \\ 1 + x\cos \theta + x^2 \cos(2\theta) + x^3\cos(3\theta) + x^4\cos(4\theta) + \dots = 1$

obliviousninja · Dec 11, 2013

Re: HSC 2014 4U Marathon

Sy, how hard can stuff in graphing get? I never really saw anything hard.

asianese · Dec 11, 2013

Re: HSC 2014 4U Marathon

$$Using de Moivre's theorem$

$(\cos \theta + i\sin\theta)^n = \cos(n\theta) + i\sin(n\theta),$

$$show that for positive, even integers $ n$,$

$\cos(n\theta) = \sum_{k=0}^{n/2} \binom{n}{2k} (-1)^k\sin^{n-2k}\theta\cos^{2k}\theta $ \\and derive a similar expression for $ \sin(n\theta).$

(not sure if this is 100% right, just off the top of my head)

anomalousdecay · Dec 11, 2013

Re: HSC 2014 4U Marathon

asianese said:
$$Using de Moivre's theorem$

$(\cos \theta + i\sin\theta)^n = \cos(n\theta) + i\sin(n\theta),$

$$show that for positive, even integers $ n$,$

$\cos(n\theta) = \sum_{k=0}^n \binom{n}{2k} (-1)^k\sin^{n-2k}\theta\cos^{2k}\theta $ \\and derive a similar expression for $ \sin(n\theta).$

(not sure if this is 100% right, just off the top of my head)

Wasn't this from a past paper?

anomalousdecay · Dec 11, 2013

Re: HSC 2014 4U Marathon

obliviousninja said:
Sy, how hard can stuff in graphing get? I never really saw anything hard.

The hardest thing I saw was in this year's paper, and that was still pretty easy (full marks).

Also, to do the multiple choice question, you kinda had to know L'Hopital's (I forgot to use this and lost the mark).

asianese · Dec 11, 2013

Re: HSC 2014 4U Marathon

anomalousdecay said:
Wasn't this from a past paper?

It's from my head?

Make a Difference – Donate to Bored of Studies!

HSC 2013 MX2 Marathon (archive) (2 Viewers)

what is that?It is Cowpea

Σ

This too shall pass

This too shall pass

Well-Known Member

This too shall pass

This too shall pass

Queen

Σ

(╯°□°）╯━︵ ┻━┻ - - - -

Queen

Queen

This too shall pass

Σ

This too shall pass

(╯°□°）╯━︵ ┻━┻ - - - -

Σ

Premium Member

Premium Member

Σ

Users Who Are Viewing This Thread (Users: 0, Guests: 2)