glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
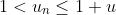
then
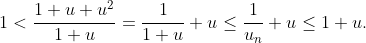
Noting that the penultimate term is just , induction does the trick.
, induction does the trick.
IfA little hard for the lower level marathon but a little easier for this level:

then
Noting that the penultimate term is just
