glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon
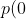+q(0)+r(0)=(b-c)+(c-a)+(a-b)=0.)
so at least one term on the LHS must be non-positive. As each of these polynomials is concave up, at least one must be concave up with vertex on below the x-axis. This polynomial must then have at least one real root.
We have
so at least one term on the LHS must be non-positive. As each of these polynomials is concave up, at least one must be concave up with vertex on below the x-axis. This polynomial must then have at least one real root.

