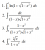Re: MX2 2015 Integration Marathon
There are interesting extensions to this: http://en.wikipedia.org/wiki/Proof_that_22/7_exceeds_π#Proof_that_355.2F113_exceeds_.CF.80
There are interesting extensions to this: http://en.wikipedia.org/wiki/Proof_that_22/7_exceeds_π#Proof_that_355.2F113_exceeds_.CF.80