Just like in real life, it'd be much more helpful if you showed your working out/progress if you want an answer which resolves your problems, otherwise people are just going to give you vague answers.
You might be confused with the algebraic manipulation and assume you just "simplify" the inequality like some random algebraic equation without no thought, DO NOTE that you're being smart with algebra and getting a simpler inequality to work with moreso than JUST solving 2/x+1 <= 1 without thought (which is easy later on once your comfortable with functions). You actually have to pay attention to the inequality and some critical points.
2/(x+1) <= 1
DO NOTE THAT x != -1 here since 2/0, this means that f(x) = 2/(x+1) is undefined on x = 1 and so you have to factor that in.
2(x+1) <= (x+1)^2 (multiply both sides by (x+1)^2 to maintain sign of inequality)
2x + 2 <= x^2 + 2x + 1
0 <= x^2 - 1
(x-1)(x+1) >= 0
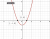
An easy way to get the solutions and a way to avoid silly mistakes is to visualise the parabola with x intercept x = 1 and x = -1. In this case, the function x^2 - 1 where it is >= 0 would be x <= -1 and x >= 1 (as seen above) if you were
just purely solving the inequality but you are not solving x^2 - 1 >= 0, you are solving 2/x+1 <= 1 so you need to factor in the condition x != -1.
But remember that you are using algebraic manipulation to get a simpler inequality and that x != -1 is established beforehand since in the original equation you're finding 2/(x+1) <= 1 so it is always noted that x != -1 OR else it is not defined since that would mean 2/(x+1) = 2/0 at x = -1 which is ofc undefined. So as a result, the bound is actually open on x = -1 since x = -1 is undefined and HENCE x < -1 INSTEAD of x <= -1. At x = 1, there is no such issues so x = 1 is a closed point i.e x >= 1.
Therefore x < -1 and x >= 1 is the answer.
Its the same reason why f(x) = x/x is not the same as f(x) = 1 for x from -infinity to infinity due to it not being defined on x = 0 i.e f(0) = 0/0.


