For question 17, a polynomial
 = 0)
can inly have a multiple root if there are any

-values for which
 = P'(x) = 0)
, using the multiple root theorem. If you attempt to solve the equation
 = P'(x))
, you should find it has only one solution,
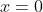
. However,
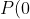 = 1 \neq 0)
and so the only potential multiple root isn't a root at all, and so there are no multiple roots.
In fact, if
)
is extended to an infinite polynomial, it is the polynomial version of
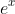
, as indicated by the fact that you then have
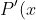 = P'(x))
and thus there are no zeroes of
 = 0)
at all.