fatima96
Member
Hey people!
So like yeah I forgot how to sketch hyperbolas like these ones :
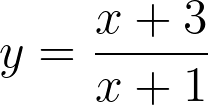
So like yeah I forgot how to sketch hyperbolas like these ones :
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
There is no polynomial division in 2U.Change x+3/x+1 to 1 + [2/(x+1)] and graph from there
Oh sorry,There is no polynomial division in 2U.
I'm not sure of 2U way, but you should know that there is a restriction on x = -1.
You make the denominator equal to 0 so x+1 = 0 so x = -1 (that's your vertical asymptote)Hey people!
So like yeah I forgot how to sketch hyperbolas like these ones :
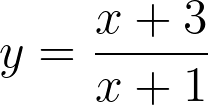
You don't need polynomial division for this simple transformation.There is no polynomial division in 2U.
I'm not sure of 2U way, but you should know that there is a restriction on x = -1.
Question, how is this more superior than to just sub in x = 0, y = 0, x -> ±infinity, and finding the vertical asymptote?Change x+3/x+1 to 1 + [2/(x+1)] and graph from there
^ Exactly what I wanted to say.Question, how is this more superior than to just sub in x = 0, y = 0, x -> ±infinity, and finding the vertical asymptote?
You will still need to do what I just said to the 2/(x+1) term. The only real advantage is that you'll see the horizontal asymptote immediately (although, just subbing in large numbers is still an effective method).
It's not really, just an alternative method for people to recognise it as simply a hyperbola shifted up one units and two to the left.Question, how is this more superior than to just sub in x = 0, y = 0, x -> ±infinity, and finding the vertical asymptote?
You will still need to do what I just said to the 2/(x+1) term. The only real advantage is that you'll see the horizontal asymptote immediately (although, just subbing in large numbers is still an effective method).

